Cho hình vuông ABCD cạnh bằng 2. Điểm M nằm trên đoạn thẳng AC sao cho AM = AC/4. Gọi N là trung điểm của đoạn thẳng DC. Tính vecto MB . vecto MN. A. –4; B. 0; C. 4; D. 16.
Câu hỏi:
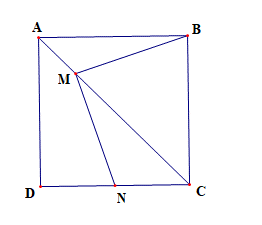
Cho hình vuông ABCD cạnh bằng 2. Điểm M nằm trên đoạn thẳng AC sao cho \[{\rm{A}}M = \frac{{AC}}{4}\]. Gọi N là trung điểm của đoạn thẳng DC. Tính \(\overrightarrow {MB} .\overrightarrow {MN} \).
A. –4;
B. 0;
C. 4;
D. 16.
Trả lời:
Lời giải
Đáp án đúng là: B
Ta có: \(MB = \overrightarrow {AB} - \overrightarrow {AM} = \overrightarrow {AB} - \frac{1}{4}\overrightarrow {AC} \)
\( = \overrightarrow {AB} - \frac{1}{4}(\overrightarrow {AB} + \overrightarrow {AD} ) = \frac{3}{4}\overrightarrow {AB} - \frac{1}{4}\overrightarrow {AD} \)
\(\overrightarrow {MN} = \overrightarrow {AN} - \overrightarrow {AM} = \overrightarrow {AD} + \overrightarrow {DN} - \frac{1}{4}\overrightarrow {AC} \)
\( = \overrightarrow {AD} + \frac{1}{2}\overrightarrow {DC} - \frac{1}{4}(\overrightarrow {AB} + \overrightarrow {AD} )\)
\( = \overrightarrow {AD} + \frac{1}{2}\overrightarrow {AB} - \frac{1}{4}(\overrightarrow {AB} + \overrightarrow {AD} )\)
\( = \frac{3}{4}\overrightarrow {AD} + \frac{1}{4}\overrightarrow {AB} \)
Suy ra \(\overrightarrow {MB} .\overrightarrow {MN} = \left( {\frac{3}{4}\overrightarrow {AB} - \frac{1}{4}\overrightarrow {AD} } \right)\left( {\frac{3}{4}\overrightarrow {AD} + \frac{1}{4}\overrightarrow {AB} } \right)\)
\( = \frac{1}{{16}}\left( {3\overrightarrow {AB} .\overrightarrow {AD} + 3{{\overrightarrow {AB} }^2} - 3{{\overrightarrow {AD} }^2} - \overrightarrow {AD} .\overrightarrow {AB} } \right)\)
\( = \frac{1}{{16}}\left( {0 + 3{a^2} - 3{a^2} - 0} \right) = 0\).
Vậy ta chọn đáp án B.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho tam giác ABC cân tại A nội tiếp đường tròn tâm O. Gọi D là trung điểm của AB, E là trọng tâm tam giác ACD. Chứng minh rằng OE vuông góc với CD.
Xem lời giải »
Câu 2:
Cho hình vuông ABCD có cạnh bằng 2. Tính \(T = \left| {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {A{\rm{D}}} } \right|\).
Xem lời giải »
Câu 3:
Cho tam giác ABC cân tại A, O là trung điểm của BC. Vẽ đường tròn tâm O tiếp xúc với AB, AC tại H và K. Lấy E bất kỳ thuộc cung nhỏ HK. Vẽ tiếp tuyến tại E cắt AB, AC ở M, N.
a) Giả sử \(\widehat B = \widehat C = \alpha \). Tính \(\widehat {MON}\).
b) Chứng minh rằng OM, ON chia tứ giác BMNC thành ba tam giác đồng dạng.
c) Giả sử BC = 2a. Tính BM . CN.
d) MN ở vị trí nào thì tổng BM + CN nhỏ nhất?
Xem lời giải »
Câu 4:
Cho tam giác ABC cân tại A, đường cao AH. Gọi I là trung điểm AB, K là điểm đối xứng với H qua điểm I.
a) Tứ giác ACHI là hình gì ? Vì sao?
b) Tứ giác AHBK là hình gì ? Vì sao?
c) Nếu tam giác ABC đều thì ACHI là hình gì?
d) Tam giác ABC có điều kiện gì thì AHBK là hình vuông.
Xem lời giải »
Câu 5:
Cho tam giác ABC vuông tại B (AB < AC) có AM là tia phân giác (M ∈ BC), trên cạnh AC lấy điểm N sao cho AB = AN.
a) Chứng minh ∆ABM = ∆ANM.
b) Chứng minh \(\widehat {BAC} = \widehat {CMN}\).
Xem lời giải »


