Cho tam giác ABC cân tại A, O là trung điểm của BC. Vẽ đường tròn tâm O tiếp xúc với AB, AC tại H và K. Lấy E bất kỳ thuộc cung nhỏ HK. Vẽ tiếp tuyến tại E cắt AB, AC ở M, N. a) Giả sử góc B

Cho tam giác ABC cân tại A, O là trung điểm của BC. Vẽ đường tròn tâm O tiếp xúc với AB, AC tại H và K. Lấy E bất kỳ thuộc cung nhỏ HK. Vẽ tiếp tuyến tại E cắt AB, AC ở M, N.

a) Giả sử \(\widehat B = \widehat C = \alpha \). Tính \(\widehat {MON}\).

b) Chứng minh rằng OM, ON chia tứ giác BMNC thành ba tam giác đồng dạng.

c) Giả sử BC = 2a. Tính BM . CN.

d) MN ở vị trí nào thì tổng BM + CN nhỏ nhất?

Lời giải

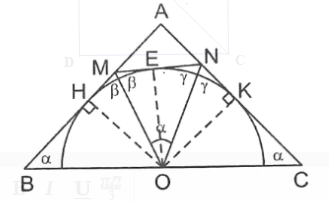
a) Xét tam giác ABC có

\(\widehat A + \widehat B + \widehat C = 180^\circ \) (tổng ba góc trong một tam giác)

Hay \(\widehat A + \alpha + \alpha = 180^\circ \)

Suy ra \(\widehat A = 180^\circ - 2\alpha \)

Xét tứ giác AHOK có

\(\widehat {AHO} + \widehat {AK{\rm{O}}} = 90^\circ + 90^\circ = 180^\circ \)

Suy ra tứ giác AHOK nội tiếp

Do đó \(\widehat {HAK} + \widehat {HOK} = 180^\circ \)

Hay \(180^\circ - 2\alpha + \widehat {HOK} = 180^\circ \)

Suy ra \(\widehat {HOK} = 2\alpha \)

Xét (O) có MH, ME là hai tiếp tuyến cắt nhau tại M

Suy ra OM là tia phân giác của \(\widehat {HOE}\)

Do đó \(\widehat {HOM} = \widehat {MOE} = \frac{1}{2}\widehat {HOE}\)

Xét (O) có NK, NE là hai tiếp tuyến cắt nhau tại N

Suy ra ON là tia phân giác của \(\widehat {KOE}\)

Do đó \(\widehat {KON} = \widehat {NOE} = \frac{1}{2}\widehat {KOE}\)

Ta có: \(\widehat {MON} = \widehat {MOE} + \widehat {NOE} = \frac{1}{2}\widehat {HOE} + \frac{1}{2}\widehat {K{\rm{O}}E} = \frac{1}{2}\widehat {HOK} = \frac{1}{2}.2\alpha = \alpha \)

Vậy \(\widehat {MON} = \alpha \)

b) Xét (O) có MH, ME là hai tiếp tuyến cắt nhau tại M

Suy ra MO là tia phân giác của \(\widehat {HME}\)

Do đó \(\widehat {HMO} = \widehat {OME} = \frac{1}{2}\widehat {HME}\)

Xét (O) có NK, NE là hai tiếp tuyến cắt nhau tại N

Suy ra NO là tia phân giác của \(\widehat {KNE}\)

Do đó \(\widehat {KNO} = \widehat {ONE} = \frac{1}{2}\widehat {KNE}\)

Xét ∆BMO và ∆OMN có:

\(\widehat {BMO} = \widehat {NMO}\) (chứng minh trên);

\(\widehat B = \widehat {MON}\left( { = \alpha } \right)\)

Suy ra (g.g)

Xét ∆CON và ∆OMN có

\(\widehat {CNO} = \widehat {MNO}\) (chứng minh trên);

\(\widehat C = \widehat {MON}\left( { = \alpha } \right)\)

Suy ra (g.g)

Vậy OM, ON chia tứ giác BMNC thành ba tam giác đồng dạng.

c) Vì OM, ON chia tứ giác BMNC thành ba tam giác đồng dạng

Suy ra

Do đó \(\frac{{CO}}{{BM}} = \frac{{CN}}{{BO}}\)

Suy ra BM . CN = CO . BO = a . a = a²

d) Vì tích BM . CN = a² cố định nên tổng BM + CN nhỏ nhất khi BM = CN

Mà AB = AC

Suy ra \(\frac{{BM}}{{AB}} = \frac{{CN}}{{AC}}\)

Do đó MN // BC

Vậy khi MN // BC thì BM + CN nhỏ nhất.