Cho lăng trụ đứng ABC.A'B'C' có chiều cao bằng 4, đáy ABC là tam giác cân tại
Câu hỏi:
Cho lăng trụ đứng ABC.A'B'C' có chiều cao bằng 4, đáy ABC là tam giác cân tại A với AB = AC = 2; \[\widehat {BAC} = 120^\circ \]. Tính bán kính mặt cầu ngoại tiếp lăng trụ trên.
Trả lời:
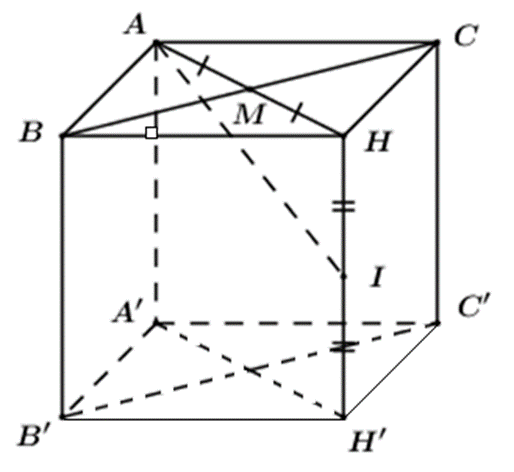
Gọi M là trung điểm của BC, H là điểm đối xứng với A qua M.
Xét tứ giác ABHC có hai đường chéo cắt nhau tại trung điểm mỗi đường và AM ⊥ BC
Þ AH ⊥ BC (do tam giác ABC cân tại A) nên ABHC là hình thoi
Þ HB = HC.
Xét tam giác ABH có AB = BH, \[\widehat {BAH} = \frac{1}{2}\widehat {BAC} = 60^\circ \]nên là tam giác đều, do đó HA = HB.
Suy ra HA = HB = HC hay H là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi H’ là hình chiếu của A lên (A’B’C’) thì H’ chính là tâm đường tròn ngoại tiếp tam giác A’B’C’, khi đó HH’ là trục của khối lăng trụ đứng.
Gọi I là trung điểm của HH’, ta có IA = IB = IC, IA’ = IB’ = IC’.
Xét tam giác vuông AHI và tam giác vuông A’H’I có:
HI = H’I (I là trung điểm của HH’)
AH = A’H’
\[\widehat {AHI} = \widehat {A'H'I'} = 90^\circ \]
Þ ΔAHI = ΔA′H′I (c.g.c)
Þ IA = IA′
Do đó IA = IB = IC = IA’ = IB’ = IC’ hay I chính là tâm mặt cầu ngoại tiếp khối lăng trụ đứng ABC.A’B’C’.
Ta có AH = AB = 2 (do ABHC là hình thoi) và HH’ = AA’ = 4 nên IH = 2.
Áp dụng định lí Py-ta-go trong tam giác vuông AHI, ta có:
\[AI = \sqrt {A{H^2} + H{I^2}} = \sqrt {{2^2} + {2^2}} = 2\sqrt 2 \]
Vậy bán kính mặt cầu ngoại tiếp khối lăng trụ là \[R = 2\sqrt 2 \].


