Cho lục giác đều ABCDEF và O là tâm của nó. Đẳng thức nào sau đây sai
Câu hỏi:
Cho lục giác đều ABCDEF và O là tâm của nó. Đẳng thức nào sau đây sai?
A. \(\overrightarrow {OA} + \overrightarrow {OC} + \overrightarrow {OE} = 0.\)
B. \(\overrightarrow {BC} + \overrightarrow {FE} = \overrightarrow {AD} \).
C. \(\overrightarrow {OA} + \overrightarrow {OC} + \overrightarrow {OB} = \overrightarrow {EB} .\)
D. \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EF} = 0.\)
Trả lời:
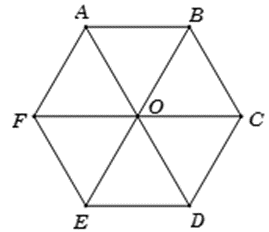
Ta có OABC là hình bình hành.
\( \Rightarrow \overrightarrow {OA} + \overrightarrow {OC} + \overrightarrow {OE} = \overrightarrow {OB} + \overrightarrow {OE} = \vec 0\) ( O là trung điềm của BE ). Do đó A đúng
Ta có: \(\overrightarrow {BC} = \overrightarrow {AO} \) (ABCO là hình bình hành)
\(\overrightarrow {FE} = \overrightarrow {OD} \) (FODE là hình bình hành)
Suy ra \(\overrightarrow {BC} + \overrightarrow {FE} = \overrightarrow {AO} + \overrightarrow {OD} = \overrightarrow {AD} \). Do đó B đúng
Ta có \({\rm{OABC}}\) là hình bình hành
\( \Rightarrow \overrightarrow {OA} + \overrightarrow {OC} + \overrightarrow {OB} = \overrightarrow {OB} + \overrightarrow {OB} = 2\overrightarrow {OB} \). Do đó C đúng.

