Cho tứ diện ABCD có thể tích bằng 12 và G là trọng tâm của tam giác BCD
Câu hỏi:
Cho tứ diện ABCD có thể tích bằng 12 và G là trọng tâm của tam giác BCD. Tính thể tích V của khối chóp A.GBC
A. V = 3.
B. V = 4.
C. V = 5.
D. V = 6.
Trả lời:
Đáp án đúng là: B
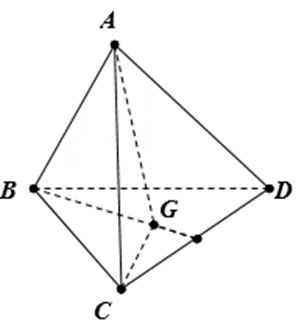
Tứ diện ABCD và khối chóp A.GBC có cùng đường cao là khoảng cách từ A đến mặt phẳng (BCD). Do G là trọng tâm tam giác BCD nên ta có S∆BGC = S∆BGD = S∆CGD ⇒ S∆BCD = 3SBGC.
Áp dụng công thức thể tích hình chóp ta có:
\(\left. {\begin{array}{*{20}{c}}{{V_{A.BCD}} = \frac{1}{3}h \cdot {S_{\Delta BCD}}}\\{{V_{A.GBC}} = \frac{1}{3}h \cdot {S_{\Delta GBC}}}\end{array}} \right\} \Rightarrow \frac{{{V_{A.BCD}}}}{{{V_{A.GBC}}}} = \frac{{\frac{1}{3}h \cdot {S_{\Delta BCD}}}}{{\frac{1}{3}h \cdot {S_{\Delta GBC}}}} = \frac{{{S_{\Delta BCD}}}}{{{S_{\Delta GBC}}}} = 3\)
\( \Rightarrow {V_{A.GBC}} = \frac{1}{3}{V_{ABCD}} = \frac{1}{3}.12 = 4.\)

