Cho tam giác ABC có trọng tâm G và hai trung tuyến AM, BN. Biết AM=15, BN
Câu hỏi:
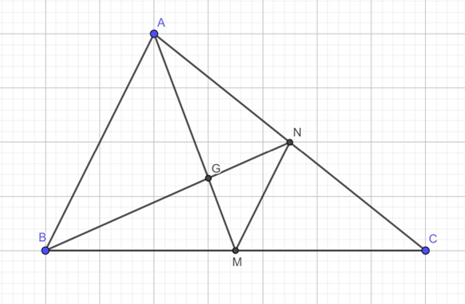
Cho tam giác ABC có trọng tâm G và hai trung tuyến AM, BN. Biết AM=15, BN = 12 và tam giác CMN có diện tích là \[15\sqrt 3 \]. Tính độ dài đoạn thẳng MN
Trả lời:
\[{S_{ABC}} = \frac{1}{2} \cdot AC \cdot BC \cdot \sin \widehat {ACB}\]
\[{S_{CMN}} = \frac{1}{2} \cdot CM \cdot CN.\sin \widehat {ACB} = \frac{1}{2} \cdot \frac{1}{2}AC \cdot \frac{1}{2}BC \cdot \sin \widehat {ACB}\]
Nên \({S_{CMN}} = \frac{1}{4}{S_{ABC}}\)
\( \Rightarrow {S_{ABC}} = 4{S_{CMN}} = 60\sqrt 3 \)
\({S_{ABG}} = \frac{2}{3}{S_{ABM}} = \frac{2}{3} \cdot \frac{1}{2}{S_{ABC}} = \frac{1}{3} \cdot 60\sqrt 3 = 20\sqrt 3 \)
Lại có: \({S_{ABG}} = \frac{1}{2} \cdot AG \cdot GB \cdot {\rm{sin}}\widehat {AGB}\)
\( = \frac{1}{2} \cdot \frac{2}{3}AM \cdot \frac{2}{3}BN \cdot {\rm{sin}}\widehat {AGB} = 40 \cdot {\rm{sin}}\widehat {AGB}\)
Suy ra \(40 \cdot {\rm{sin}}\widehat {AGB} = 20\sqrt 3 \)
\( \Rightarrow {\rm{sin}}\widehat {AGB} = \frac{{\sqrt 3 }}{2}\)
\( \Rightarrow \widehat {AGB} = 60^\circ \)
Ta có: \(A{B^2} = A{G^2} + G{B^2} - 2 \cdot AG \cdot GB \cdot {\rm{cos}}\widehat {AGB}\)
\( = {\left( {\frac{2}{3} \cdot 15} \right)^2} + {\left( {\frac{2}{3} \cdot 12} \right)^2} - 2 \cdot \frac{2}{3}15 \cdot \frac{2}{3} \cdot 12 \cdot {\rm{cos}}60^\circ = 84\)
\( \Rightarrow AB = 2\sqrt {21} \)
M, N là trung điểm của BC, AC
⇒ MN là đường trung bình của ∆ACB
\( \Rightarrow MN = \frac{1}{2} \cdot AB = \frac{1}{2} \cdot 2\sqrt {21} = \sqrt {21} \)
Vậy \(MN = \sqrt {21} .\)

