Cho ngũ giác ABCDE. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DE
Câu hỏi:
Cho ngũ giác ABCDE. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DE. Gọi I và J lần lượt là trung điểm của MP và NQ. Chứng minh IJ song song với AE và \[{\rm{IJ}} = \frac{1}{4}A{\rm{E}}\].
Trả lời:
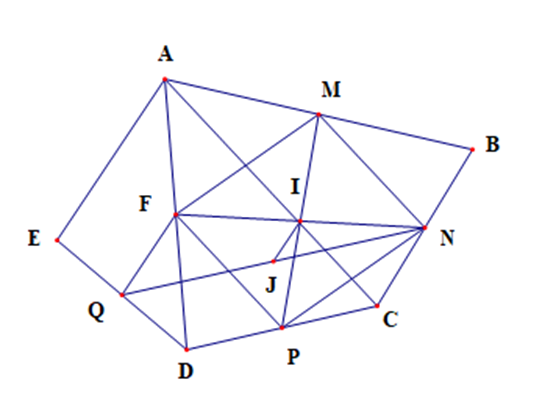
Gọi F là trung điểm của AD
Xét tam giác ABC có
M, N lần lượt là trung điểm của AB, BC
Suy ra MN là đường trung bình
Do đó \(\left\{ \begin{array}{l}MN//AC\\MN = \frac{1}{2}AC\end{array} \right.\) (1)
Xét tam giác ADC có
P, F lần lượt là trung điểm của CD, AD
Suy ra PF là đường trung bình
Do đó \(\left\{ \begin{array}{l}PF//AC\\PF = \frac{1}{2}AC\end{array} \right.\) (2)
Từ (1) và (2) suy ra MN // PF và MN = PF
Do đó MNPF là hình bình hành
Suy ra MP cắt FN tại trung điểm của mỗi đường
Mà I là trung điểm của MP
Suy ra I là trung điểm của FN
Xét tam giác NFQ có
I và J lần lượt là trung điểm của FN và NQ
Suy ra IJ là đường trung bình
Do đó IJ // QF và \[{\rm{IJ}} = \frac{1}{2}FQ\]
Xét tam giác AED có
F và Q lần lượt là trung điểm của AD và ED
Suy ra FQ là đường trung bình
Do đó AE // QF và \[FQ = \frac{1}{2}A{\rm{E}}\]
Mà IJ // QF (chứng minh trên)
Suy ra IJ // AE
Ta có \[{\rm{IJ}} = \frac{1}{2}FQ = \frac{1}{2}.\frac{1}{2}A{\rm{E}} = \frac{1}{4}A{\rm{E}}\]
Vậy IJ // AE và \[{\rm{IJ}} = \frac{1}{4}A{\rm{E}}\].


