Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh: a) AB^2 = BH . BC

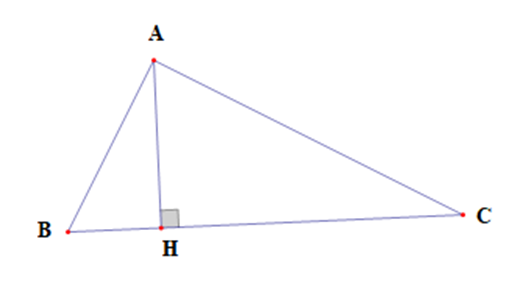
a) Xét tam giác ABC và tam giác HBA có:

\(\widehat {BAC} = \widehat {AHB} = 90^\circ \)

\(\widehat B\) là góc chung

Suy ra  (g.g)

Do đó \(\frac{{AB}}{{BH}} = \frac{{BC}}{{AB}}\)

Suy ra AB² = BH . BC

b) Xét tam giác ABC và tam giác HAC có:

\(\widehat {BAC} = \widehat {AHC} = 90^\circ \)

\(\widehat C\) là góc chung

Suy ra  (g.g)

Do đó \(\frac{{AC}}{{CH}} = \frac{{BC}}{{AC}}\)

Suy ra AC² = BC . CH

c) Vì (chứng minh câu a)

Nên \(\frac{{AH}}{{AC}} = \frac{{AB}}{{BC}}\)

Suy ra \(\frac{{A{H^2}}}{{A{C^2}}} = \frac{{A{B^2}}}{{B{C^2}}}\)                       (1)

Vì (chứng minh câu b)

Nên \(\frac{{BC}}{{AC}} = \frac{{AB}}{{AH}}\)

Suy ra \(\frac{{A{H^2}}}{{A{B^2}}} = \frac{{A{C^2}}}{{B{C^2}}}\)                       (2)

Từ (1) và (2) suy ra \(\frac{{A{H^2}}}{{A{C^2}}} + \frac{{A{H^2}}}{{A{B^2}}} = \frac{{A{B^2}}}{{B{C^2}}} + \frac{{A{C^2}}}{{B{C^2}}} = \frac{{A{B^2} + A{C^2}}}{{B{C^2}}}\)

Mà tam giác ABC vuông tại A nên BC² = AB² + AC²

Do đó \(\frac{{A{H^2}}}{{A{C^2}}} + \frac{{A{H^2}}}{{A{B^2}}} = 1\)

Suy ra \(\frac{1}{{A{C^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{A{H^2}}}\)

Vậy \(\frac{1}{{A{C^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{A{H^2}}}\).