Cho nửa đường tròn tâm O, đường kính AB và dây cung CD không song song với AB. Gọi H và K là hình chiếu của A và B trên CD. Gọi E là giao điểm của BK với nửa đường tròn (O) và I là trung điểm
Câu hỏi:
Cho nửa đường tròn tâm O, đường kính AB và dây cung CD không song song với AB. Gọi H và K là hình chiếu của A và B trên CD. Gọi E là giao điểm của BK với nửa đường tròn (O) và I là trung điểm của CD.
a) Chứng minh OI ⊥ AE.
Trả lời:
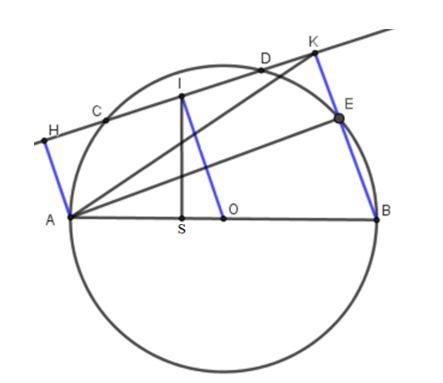
a) Ta có OC = OD ⇒ Tam giác OCD cân tại O
Mà I là trung điểm của CD ⇒ OI ⊥ CD
Xét tam giác ABE có OA = OE = OB ⇒ Tam giác EAB vuông tại E
⇒ AE ⊥ BK
BK ⊥ CD ⇒ AE // CD ⇒ OI ⊥ AE (ĐPCM)