Cho số phức z thỏa mãn |z − 4 − i| = |z + i|. Gọi z = a + bi (a; b Î ℝ) là số phức thỏa mãn
Câu hỏi:
Cho số phức z thỏa mãn |z − 4 − i| = |z + i|. Gọi z = a + bi (a; b Î ℝ) là số phức thỏa mãn |z − 1 + 3i| nhỏ nhất. Giá trị của biểu thức T = 2a + 3b là:
Trả lời:
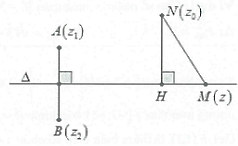
Đặt M (z); A(4; 1), B(0; −1) là các điểm biểu diễn số phức z; 4 + i và −i.
Khi đó từ giả thiết suy ra MA = MB, tập hợp điểm biểu diễn số phức z là đường trung trực của AB đi qua I(2; 0) và có VTPT là
Þ ∆: −4(x − 2) − 2y = 0
Þ ∆: 2x + y − 4 = 0
Gọi N(1; −3) là điểm biểu diễn số phức 1 − 3i
Ta có |z − 1 + 3i| nhỏ nhất khi MNmin khi M là hình chiếu vuông góc của N trên ∆, suy ra MN: x − 2y + 1 = 0
Giải hệ phương trình
Þ M(3; −2)
Þ z = 3 − 2i
Khi đó T = 2a + 3b = 2.3 + 3.(−2) = 0.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Đa thức P (x) = 32x5 − 80x4 + 80x3 − 40x2 + 10x − 1 là khai triển của nhị thức nào dưới đây?
Xem lời giải »
Câu 2:
Cho đoạn thẳng AB. Vị trí của điểm M thỏa mãn: được xác định bởi:
Xem lời giải »
Câu 3:
Cho hai điểm A, B phân biệt. Xác định điểm M biết .
Xem lời giải »
Câu 4:
Cho a, b, c là 3 cạnh trong tam giác. Chứng minh rằng: .
Xem lời giải »
Câu 5:
Cho các số phức z thỏa mãn |z − 2i| = |z + 2|. Gọi z là số phức thỏa mãn |(2 − i)z + 5| nhỏ nhất. Khi đó:
Xem lời giải »
Câu 7:
Trong mặt phẳng với hệ tọa độ Oxy, cho các điểm A(4; 0), B(1; 4) và C(1; −1). Gọi G là trọng tâm tam giác ABC. Biết rằng G là điểm biểu diễn số phức z. Mệnh dề nào sau đây là đúng?
Xem lời giải »
Câu 8:
Trong mặt phẳng Oxy cho tam giác ABC với A(1; 3), B(2; −4), C(3; −2) và điểm G và trọng tâm tam giác ABC. Ảnh G' của G qua phép đối xứng trục Ox có tọa độ là:
Xem lời giải »


