Cho tam giác ABC (AB < AC) có ba góc nhọn nội tiếp trong đường tròn tâm O
Câu hỏi:
Cho tam giác ABC (AB < AC) có ba góc nhọn nội tiếp trong đường tròn tâm O, bán kính R. Gọi H là giao điểm của ba đường cao AD, BE, CF của tam giác ABC.
a) Chứng minh rằng AEHF và AEDB là các tứ giác nội tiếp đường tròn.
b) Vẽ đường kính AK của đường tròn (O). Chứng minh tam giác ABD và tam giác AKC đồng dạng với nhau. Suy ra AB.AC = 2R.AD.
c) Chứng minh OC vuông góc với DE.
Trả lời:
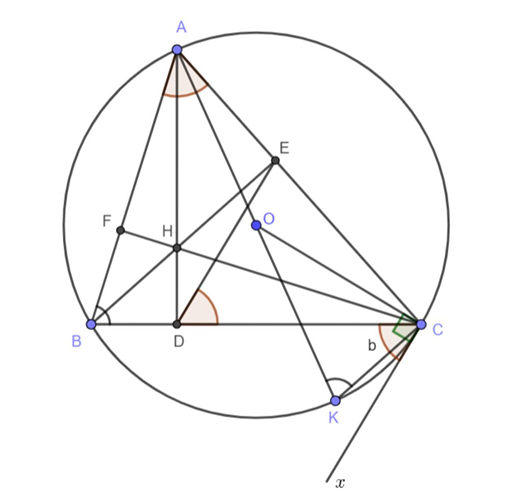
a) Ta có: BE, CF là đường cao của ΔABC nên BE ⊥ AC, CF ⊥ AB
⇒ \(\widehat {AEH} = \widehat {AFH} = 90^\circ \)
Tứ giác AEHF có: \(\widehat {AEH} + \widehat {AFH} = 90^\circ + 90^\circ = 180^\circ \) mà chúng ở vị trí đối đỉnh nên AEHF là tứ giác nội tiếp đường tròn đường kính (AH)
Ta có: \(\widehat {AEB} = \widehat {ADB} = 90^\circ \)
⇒ E, D cùng nhìn cạnh AB dưới góc 90 độ nên AEDB nội tiếp đường tròn đường kính (AB)
b) Xét ΔABD và ΔAKC có:
\(\widehat {ABD} = \widehat {AKC}\) (góc nội tiếp cùng chắn cung AC)
\(\widehat {ADB} = \widehat {ACK} = 90^\circ \)
⇒ ΔABD ∽ ΔAKC (g.g)
⇒ \(\frac{{AB}}{{AK}} = \frac{{AD}}{{AC}}\)
⇒ AB.AC = AK.AD = AD.2R
c) Dựng Cx ⊥ OC hay Cx là tiếp tuyến của (O)
⇒ \(\widehat {BCx} = \widehat {BAC}\) (góc tạo bởi tiếp tuyến và dây cung, góc nội tiếp cùng chắn cung BC)
\(\widehat {EDC} = \widehat {BAC}\)(do AEDB nội tiếp)
⇒ \[\widehat {EDC} = \widehat {BCx}\]mà chúng ở vị trí so le trong
⇒ DE // Cx mà Cx ⊥ OC
⇒ DE ⊥ OC.

