Cho tam giác ABC (AB = AC). Kẻ đường cao AH cắt đường tròn tâm O
Câu hỏi:
Cho tam giác ABC (AB = AC). Kẻ đường cao AH cắt đường tròn tâm O ngoại tiếp tam giác tại D.
a) Chứng minh AD là đường kính.
b) Tính .
c) Biết AB = AC = 20 cm, BC = 24 cm. Tính bán kính của đường tròn tâm (O)
Trả lời:
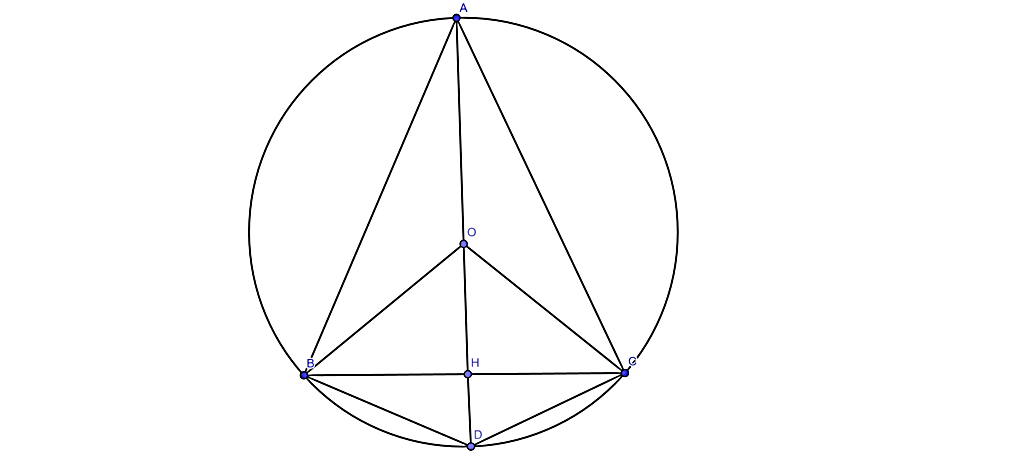
a) ΔABC có AB = AC
⇒ ΔABC cân tại A
⇒ AH là đường cao, trung tuyến, phân giác và cũng là đường trung trực của BC
Mà tâm đường tròn ngoại tiếp tam giác là giao 3 đường trung trực
⇒ O ∈ AH
⇒ AD là đường kính (đpcm)
b) ΔACD nội tiếp đường tròn đường kính AD
⇒ ΔACD vuông tại C
⇒ = 90°
c) BC = 24cm ⇒ BH = CH = 12cm
ΔABH vuông tại H
⇒ AH =
ΔABD vuông tại B có BH là đường cao
Áp dụng hệ thức lượng ta có:
AB2 = AH.AD ⇒ 202 = 16.2.R
⇒ R = 12,5cm.

