Cho tam giác ABC có AB = a, AC = 2a. Gọi D là trung điểm AC, M là điểm thỏa mãn
Câu hỏi:
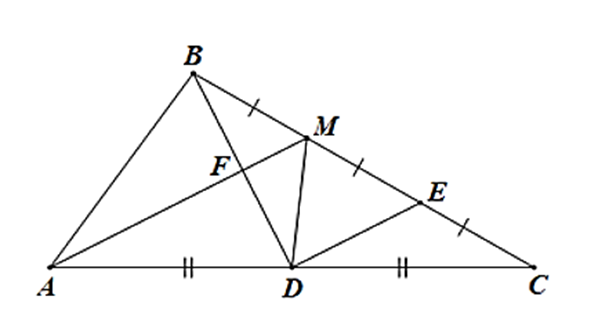
Cho tam giác ABC có AB = a, AC = 2a. Gọi D là trung điểm AC, M là điểm thỏa mãn \[\overrightarrow {BM} = \frac{1}{3}\overrightarrow {BC} \]. Chứng minh: BD vuông góc AM.
Trả lời:
Ta có: \[\overrightarrow {BM} = \frac{1}{3}\overrightarrow {BC} \]
Suy ra: BM =\(\frac{1}{3}\)BC và M thuộc BC
Lấy E là trung điểm MC
Suy ra: EM = EC = \(\frac{1}{2}\)MC = \(\frac{1}{2}.\frac{2}{3}BC = \frac{1}{3}BC\)
Nên BM = ME = EC
M là trung điểm BE.
Ta có D, E là trung điểm AC, CM
DE là đường trung bình ΔAMC
DE // AM.
Gọi AM ∩ BD = F.
DE // MF
Mà M là trung điểm BE
MF là đường trung bình ΔBDE
F là trung điểm BD
Ta có: AC = 2AB, D là trung điểm AC
AD = AB = \(\frac{1}{2}\)AC
ΔABD cân tại A.
Mà F là trung điểm BD nên ΔABD cân tại A có đường trung tuyến AM đồng thời là đường cao
Do đó AF ⊥ BD.
Suy ra AM ⊥ BD.

