Cho tam giác ABC có AB = AC. Lấy hai điểm D, E thuộc cạnh BC sao cho BD = DE = EC
Câu hỏi:
Cho tam giác ABC có AB = AC. Lấy hai điểm D, E thuộc cạnh BC sao cho BD = DE = EC. Biết AD = AE.
a) Chứng minh \(\widehat {EAB}\) = \(\widehat {DAC}\).
b) Gọi M là trung điểm của BC. Chứng minh AM là phân giác của góc \(\widehat {DAE}\).
c) Gỉa sử \(\widehat {DAE} = 60^\circ \). Tính các góc còn lại của tam giác ADE.
Trả lời:
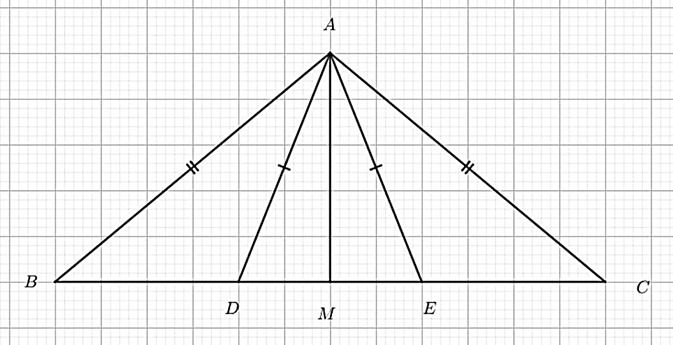
a) Ta có: BE = BD + DE = DE + DE = 2DE (do BD = DE giả thiết)
DC = DE + EC = DE + DE = 2DE (do DE = EC giải thiết)
⇒ BE = DC
Xét ΔABE và ΔACD có:
AB = AC (giả thiết)
AE = AD (giả thiết)
BE = CD (chứng minh trên)
⇒ ΔABE = ΔACD (c.c.c)
⇒ \(\widehat {EAB} = \widehat {DAC}\) (2 góc tương ứng)
b) Ta có M là trung điểm cạnh BC ⇒ AM = CM
Và BD = EC (giả thiết)
Ta có: DM = BM − BD
EM = CM − CE
⇒ DM = EM (vì cùng bằng hiệu của các cạnh bằng nhau)
Xét ΔADM và ΔAEM ta có:
AM chung
AD = AE (giả thiết)
DM = EM (chứng minh trên)
⇒ ΔADM = ΔAEM (c.c.c)
⇒ \[\widehat {DAM} = \widehat {EAM}\] (2 góc tương ứng)
⇒ AM chia \(\widehat {DAE}\) thành 2 góc bằng nhau (\(\widehat {DAM} = \widehat {EAM}\))
⇒ AM là phân giác \(\widehat {DAE}\)(đpcm)
c) ΔADM = ΔAEM
⇒ \(\widehat {ADM} = \widehat {AEM}\) (hai góc tương ứng)
Hay \(\widehat {ADE} = \widehat {AED}\)
Áp dụng tính chất tổng 3 góc trong ΔADE ta có:
\(\widehat {DAE} + \widehat {ADE} + \widehat {AED} = 180^\circ \)
⇒ \(60 + 2\widehat {ADE} = 180^\circ \)
⇒ \(\widehat {ADE} = 60^\circ \)
ΔADE có: \(\widehat {DAE} = \widehat {ADE} = \widehat {AED} = 60^\circ \).

