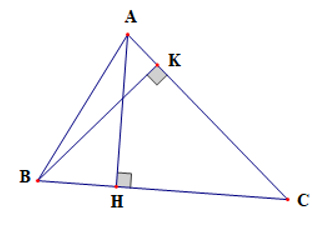
Cho tam giác ABC có ba góc nhọn, AB = c, AC = b, BC = a. Chứng minh rằng:

Câu hỏi:

\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}

Trả lời:

Cho tam giác ABC có ba góc nhọn, AB = c, AC = b, BC = a. Chứng minh rằng: (ảnh 1)

Cho tam giác ABC có ba góc nhọn, AB = c, AC = b, BC = a. Chứng minh rằng: (ảnh 2)

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Xác định số hữu tỉ a sao cho x³ + ax² + 5x + 3 chia hết cho x² + 2x + 3.

Xem lời giải »

Câu 2:

Xét sự biến thiên của hàm số y = tan2x trên một chu kì tuần hoàn. Trong các kết luận sau, kết luận nào đúng?

A. Hàm số đã cho đồng biến trên khoảng $(0; \frac{π}{4})$ và $(\frac{π}{4}; \frac{π}{2})$ .

B. Hàm số đã cho đồng biến trên khoảng $(0; \frac{π}{4})$ và nghịch biến trên khoảng $(\frac{π}{4}; \frac{π}{2})$

C. Hàm số đã cho luôn đồng biến trên khoảng $(0; \frac{π}{2})$ .

D. Hàm số đã cho nghịch biến trên khoảng $(0; \frac{π}{4})$ và đồng biến trên khoảng $(\frac{π}{4}; \frac{π}{2})$

Xem lời giải »

Câu 3:

Tìm x thỏa mãn phương trình $\sqrt{x^{2} - x - 6} = \sqrt{x - 3} .$

A. x = 2;

B. x = 4;

C. x = 1;

D. x = 3.

Xem lời giải »

Câu 4:

Giải phương trình: x(x + 2)(x² + 2x + 2) + 1 = 0.

Xem lời giải »

Câu 5:

Tìm x: (2x – 1)² – (x + 3)² = 0.

Xem lời giải »

Câu 6:

Tính:

a) (x + 2y)²;

b) (x – 3y)(x + 3y);

c) (5 – x)² .

Xem lời giải »

Câu 7:

Tính:

a) (x – 2y)²;

b) (2x² + 3)²;

c) (x – 2)(x² + 2x + 4);

d) (2x – 1)³.

Xem lời giải »

Câu 8:

Phân tích đa thức thành nhân tử

(x² + x)² – 14(x² + x) + 24.

Xem lời giải »

❮ Bài trước Bài sau ❯

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án

Cho tam giác ABC có ba góc nhọn, AB = c, AC = b, BC = a. Chứng minh rằng:

Xem thêm bài tập Toán có lời giải hay khác: