Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia
Câu hỏi:
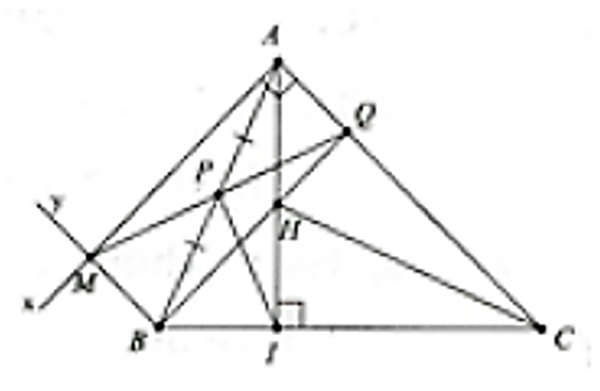
Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc với AC, từ B kẻ tia By song song với AC. Gọi M là giao điểm của tia Ax và tia By. Nối M với trung điểm P của AB, đường MP cắt AC tại Q và BQ cắt AI tại H.
a) Tứ giác AMBQ là hình gì?
b) Chứng minh rằng CH ⊥ AB.
c) Chứng minh tam giác PIQ cân.
Trả lời:
a) Ta có: \(\left\{ \begin{array}{l}\widehat {AQB} = 90^\circ \\\widehat {MAQ} = 90^\circ \\\widehat {MBQ} = 90^\circ \end{array} \right.\)
Suy ra: AMBQ là hình chữ nhật.
b) Ta có: AI ⊥ BC (giả thiết) và BQ ⊥ AC
Nên H là trực tâm của tam giác ABC
Suy ra: CH ⊥ AB
c) Ta có: PQ = \(\frac{{AB}}{2}\)(Vì PQ là đường trung tuyến ứng với cạnh huyền trong tam giác vuông ABQ)
PI = \(\frac{{AB}}{2}\)(Vì PI là đường trung tuyến ứng với cạnh huyền trong tam giác vuông ABI)
Suy ra: PQ = PI
Nên Tam giác QIP cân tại P.

