Cho tam giác ABC có góc A = 90 độ, trên cạnh BC lấy điểm E sao cho BA
Câu hỏi:
Cho tam giác ABC có \(\widehat A = 90^\circ \), trên cạnh BC lấy điểm E sao cho BA = BE. Tia phân giác góc B cắt AC ở D.
a) So sánh DA và DE.
b) Tính số đo \(\widehat {BED}\).
Trả lời:
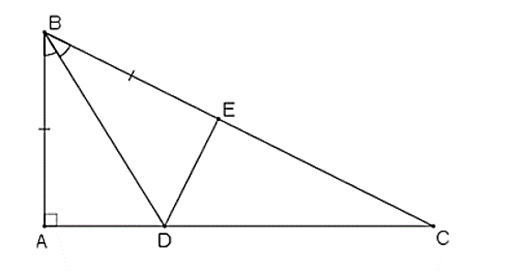
a) Xét △ABD và △EBD có:
Chung BD
\(\widehat {ABD} = \widehat {DBE}\)(vì BD là phân giác)
AB = BE
⇒ △ABD = △EBD (c.g.c)
Suy ra: DA = DE (hai cạnh tương ứng)
b) Theo phần a có △ABD = △EBD (c.g.c)
⇒ \(\widehat {BED} = \widehat {BAD} = 90^\circ \).

