Cho tam giác ABC vuông tại A. Về phía ngoài tam giác, vẽ các hình vuông ABDE
Câu hỏi:
Cho tam giác ABC vuông tại A. Về phía ngoài tam giác, vẽ các hình vuông ABDE, ACFG.
a) Chứng minh tứ giác BCGE là hình thang cân.
b) Gọi K là giao điểm của các tia DE và FG, M là trung điểm của đoạn thẳng EG. Chứng minh ba điểm K, A, M thẳng hàng.
c) Chứng minh \(\widehat {COD} = 90^\circ \).
d) Chứng minh DC, FB và AM đồng quy.
Trả lời:
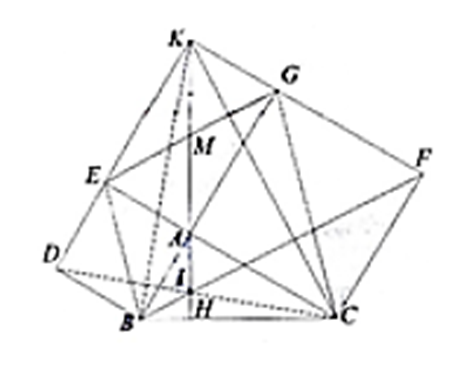
a) Vì ABDE, ACFG là các hình vuông nên ta có E, A, C thẳng hàng và B, A, G cũng thẳng hàng (1) và EC = BG.
Mà \(\widehat {EBA} = \widehat {AGC} = 45^\circ \)(2).
Từ (1) và (2):
Suy ra EB // CG và EC = BG nên EBCG là hình thang cân.
b) Ta có: \(\widehat {AEK} = \widehat {GAE} = \widehat {AGK} = 90^\circ \)
Suy ra: AEKG là hình chữ nhật, hai đường chéo EG và AK giao nhau tại trung điểm mỗi đường.
Mà M là trung điểm EG
Nên M là trung điểm AK
Suy ra: M, A, K thẳng hàng.
c) Gọi H = MA ∩ BC
Vì BEGC là hình thang cân nên ∆BEG = ∆EBC (c–g–c)
⇒ \(\widehat {ECB} = \widehat {EGB}\) mà \(\widehat {EGA} = \widehat {MAG} = \widehat {BAH}\)
⇒ \(\widehat {BAH} + \widehat {ABC} = \widehat {ECB} + \widehat {ABC} = 90^\circ \)
Suy ra: MA vuông góc với BC tại H.
d) Xét ∆ABK và ∆BDC có:
AB = DB
\(\widehat {BAK} = \widehat {DBC}\)
KA = EG = BC
Suy ra: ∆ABK = ∆BDC (c.g.c)
Suy ra: \(\widehat {BKA} = \widehat {BCD}\)
Mà KA ⊥ BC nên CD ⊥ BK
Chứng minh tương tự ta cũng có BF ⊥ KC.
Suy ra: Tam giác KBC có BF, CD, AM là 3 đường cao đồng quy tại trực tâm I.

