Cho tam giác ABC đều cạnh a, H là trung điểm của BC. Tính vecto CA - vecto HC

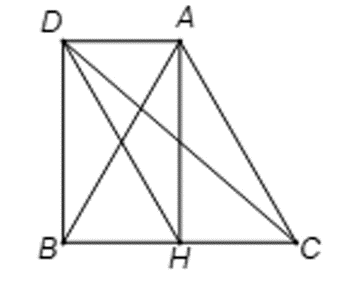
Gọi D là điềm thỏa mãn tứ giác ACHD là hình bình hành

Suy ra AD = HC, AD // HC

Mà BH = HC, AH ⊥ BC (do tam giác ABC đều có trung tuyến AH)

Do đó AHBD là hình chữ nhật

Suy ra \(\left| {\overrightarrow {CA} - \overrightarrow {HC} } \right| = \left| {\overrightarrow {CA} + \overrightarrow {CH} } \right| = \left| {\overrightarrow {CD} } \right| = CD\)

Vì tam giác BCD vuông tại B nên theo định lý Pytago ta có:

\(CD = \sqrt {B{D^2} + B{C^2}} = \sqrt {A{H^2} + B{C^2}} = \sqrt {\frac{{3{a^2}}}{4} + {a^2}} {\rm{ }} = \frac{{a\sqrt 7 }}{2}\)

Vậy ta chọn đáp án D.