Cho tam giác ABC đều cạnh a. Khi đó | vecto AB + vecto AC| bằng: A. | vecto AB + vecto AC| = a căn bậc hai của 3 . B. | vecto AB + vecto AC| = a căn bậc hai của 3/2. C. | vecto AB + vecto

❮ Bài trước Bài sau ❯

Câu hỏi:

Cho tam giác ABC đều cạnh a. Khi đó

$\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|$ bằng:

$\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 3$ .

$\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \frac{{a\sqrt 3 }}{2}$ .

$\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = 2a$ .

D. Một đáp án khác.

Trả lời:

Lời giải

Đáp án đúng là: A

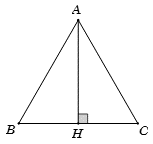
Media VietJack

Gọi H là trung điểm của BC.

Ta có tam giác ABC đều.

Suy ra AH vừa là đường trung tuyến, vừa là đường cao của tam giác ABC.

Khi đó $BH = \frac{{BC}}{2} = \frac{a}{2}$ .

Vì vậy $AH = \sqrt {A{B^2} - B{H^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}$ .

Vậy $\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {2\overrightarrow {AH} } \right| = 2.AH = 2.\frac{{a\sqrt 3 }}{2} = a\sqrt 3$ .

Do đó ta chọn phương án A.

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Biết rằng

$\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} = 1$ . Tìm giá trị thực của tham số m để hàm số

$f\left( x \right) = \left\{ \begin{array}{l}\frac{{1 + \cos x}}{{{{\left( {x - \pi } \right)}^2}}},\,\,\,\,\,\,x \ne \pi \\m,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \pi \end{array} \right.$ liên tục tại x = π.

Xem lời giải »

Câu 2:

Có bao nhiêu số tự nhiên nhỏ hơn 100 chia hết cho 2 và 3.

Xem lời giải »

Câu 3:

Chứng minh rằng với mọi góc α (0° ≤ α ≤ 180°), ta đều có sin²α + cos²α = 1.

Xem lời giải »

Câu 4:

So le ngoài là như thế nào? Lấy ví dụ.

Xem lời giải »

Câu 5:

Cho tam giác ABC đều cạnh a. Tính độ dài các vectơ