Cho tam giác ABC. Gọi M là trung điểm của AB và N là điểm trên cạnh AC sao
Câu hỏi:
Cho tam giác ABC. Gọi M là trung điểm của AB và N là điểm trên cạnh AC sao cho NC = 2NA. Gọi K là trung điểm của MN. Biểu diễn \(\overrightarrow {AK} \) theo \(\overrightarrow {AB} ,\overrightarrow {AC} \).
Trả lời:
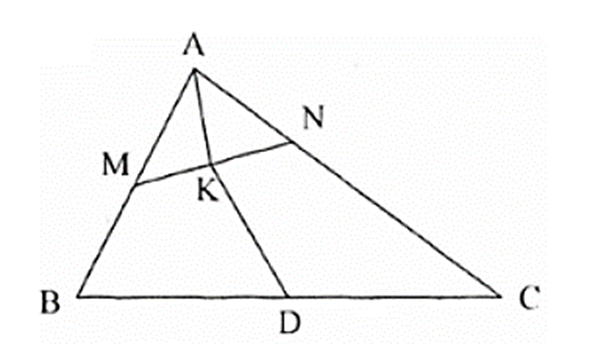
Do M là trung điểm AB nên \(\overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} \)
Vì NC = 2NA nên \(\overrightarrow {AN} = \frac{1}{3}\overrightarrow {AC} \)
Ta có: \[\overrightarrow {AK} = \frac{1}{2}\left( {\overrightarrow {AM} + \overrightarrow {AN} } \right)\](Vì K là trung điểm MN)
\[ = \frac{1}{2}.\left( {\frac{1}{2}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} } \right)\]
\[ = \frac{1}{4}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} \].

