Cho tam giác ABC nhọn, các đường cao AD, BE cắt nhau tại H. Gọi I là trung điểm của AC và J là trung điểm của BH. Xác định đường tròn đi qua ba điểm I, D, J.
Câu hỏi:
Cho tam giác ABC nhọn, các đường cao AD, BE cắt nhau tại H. Gọi I là trung điểm của AC và J là trung điểm của BH. Xác định đường tròn đi qua ba điểm I, D, J.
Trả lời:
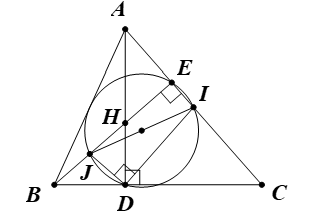
Suy ra DI = AI = IC.
Do đó tam giác ADI cân tại I.
Vì vậy ^ADI=^DAI (1)
Chứng minh tương tự, ta được ^JDH=^JHD .
Mà ^JHD=^AHE (đối đỉnh).
Suy ra ^JDH=^AHE (2)
Tam giác AHE vuông tại E: ^AHE+^HAE=90° (3)
Từ (1), (2), (3), suy ra ^JDH+^ADI=90° .
Do đó ^JDI=90°.
Vậy ba điểm I, D, J cùng thuộc một đường tròn đường kính IJ.
