Cho tam giác abc nội tiếp đường tròn (O) đường kính BC. Chứng minh rằng tam giác ABC là tam giác vuông.
Câu hỏi:
Cho tam giác abc nội tiếp đường tròn (O) đường kính BC. Chứng minh rằng tam giác ABC là tam giác vuông.
Trả lời:
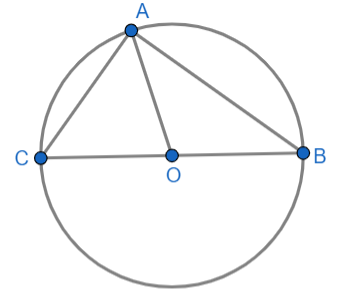
Xét tam giác ABC nội tiếp đường tròn tâm O
Ta có: OA = OB = OC (đều là bán kính của (O))
BC là đường kính nên OB = BC
Mà OA = OB nên OA = BC
Xét tam giác ABC có OA là đường trung tuyến (O là trung điểm BC)
Và OA = BC (BC là cạnh huyền)
Suy ra: ∆ABC vuông tại A.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hình thoi ABCD có cạnh bằng a và = 60°. Độ dài của vectơ ?
Xem lời giải »
Câu 2:
Cho tam giác ABC có AB = AC và M là trung điểm của BC. Gọi N là trung điểm của AB, trên tia đối của NC lấy điểm K sao cho NK = NC.
a) Chứng minh ∆ABM = ∆CMA.
b) Chứng minh AK = 2MC.
c) Tính .
Xem lời giải »
Câu 3:
Cho tam giác ABC có AB = c, BC = a, AC = b thỏa mãn: b2 + c2 – a2 = . Tính số đo .
Xem lời giải »
Câu 4:
Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 3,6 cm HC = 6,4 cm.
a) Tính AB, AC, AH.
b) Kẻ HE vuông góc AB, HF vuông góc AC. Chứng minh AB.AE = AC.AF.
Xem lời giải »
Câu 5:
Tính giá trị mỗi chữ số a,b,c biết rằng trong cùng một hàng thì giá trị của chữ số a lớn hơn giá trị của chữ số b là 2 đơn vị của hàng đó và : = 8,94.
Xem lời giải »
Câu 7:
Tìm tập xác định của hàm số y = .
Xem lời giải »
Câu 8:
Có bao nhiêu giá trị nguyên của tham số m để hàm số:
y = xác định trên ℝ?
Xem lời giải »


