Cho tam giác ABC nội tiếp đường tròn (O). Tiếp tuyến tại A cắt BC ở I
Câu hỏi:
Cho tam giác ABC nội tiếp đường tròn (O). Tiếp tuyến tại A cắt BC ở I.
a) Chứng minh: \(\frac{{IB}}{{IC}} = \frac{{A{B^2}}}{{A{C^2}}}\).
b) Tính IA, IC bắt rằng AB = 20 cm, AC = 28 cm, BC = 24 cm.
Trả lời:
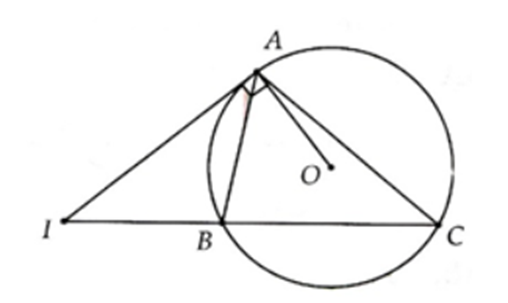
a) Xét tam giác BAI và tam giác ACI có:
Chung \(\widehat C\)
\(\widehat {ACB} = \widehat {IAB}\)(chắn cung AB nhỏ)
Suy ra: ∆BAI ~ ∆ACI (g.g)
Suy ra: \(\frac{{IB}}{{IA}} = \frac{{AB}}{{AC}}\)⇒ \[\frac{{I{B^2}}}{{I{A^2}}} = \frac{{A{B^2}}}{{A{C^2}}}\]
Mà AI là tiếp tuyến, IBC là cát tuyến nên IA2 = IB.IC
Suy ra: \[\frac{{I{B^2}}}{{IB.IC}} = \frac{{A{B^2}}}{{A{C^2}}}\]
Hay \(\frac{{IB}}{{IC}} = \frac{{A{B^2}}}{{A{C^2}}}\)
b) Vì ∆BAI ∽ ∆ACI (g.g)
Nên: \(\frac{{AI}}{{CI}} = \frac{{BI}}{{AI}}\)
⇒ \(\frac{{IA}}{{IC}} = \frac{{IC - 24}}{{IA}} = \frac{5}{7}\)
⇒ IA = 35(cm)
IC = 49 (cm).