Hình chữ nhật ABCD có diện tích 1500 m2. Tính diện tích tam giác AED
Câu hỏi:
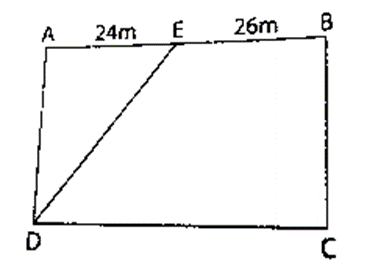
Trả lời:
Chiều dài hình chữ nhật là:
24 + 26 = 50 (m)
Chiều rộng hình chữ nhật là:
1500 : 50 = 30 (m)
Diện tích tam giác là:
30 . 24 : 2 = 360 (m²).
Câu hỏi:

Trả lời:
Chiều dài hình chữ nhật là:
24 + 26 = 50 (m)
Chiều rộng hình chữ nhật là:
1500 : 50 = 30 (m)
Diện tích tam giác là:
30 . 24 : 2 = 360 (m²).
Câu 1:
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(–1; 2); B(3; 2); C(1; 5). Tính tọa độ trọng tâm của tam giác ABC?
Câu 2:
Trong mặt phẳng Oxy cho các điểm A(–1; 2); B(5; 8) điểm M thuộc Ox sao cho tam giác MAB vuông tại A. Tính diện tích tam giác MAB?
Câu 3:
Cho các số x, y, z dương thoả mãn x2 + y2 + z2 = 1. Tìm giá trị nhỏ nhất của biểu thức M = \(\frac{1}{{16{x^2}}} + \frac{1}{{4{y^2}}} + \frac{1}{{{z^2}}}\).
Câu 4:
Tìm số lớn nhất có 4 chữ số khác nhau, chữ số hàng trăm là chữ số 5. Số này phải chia hết cho 2 và chia hết cho 5.
Câu 5:
Cho biểu thức \(M = \frac{{{x^4} + 2}}{{{x^6} + 1}} + \frac{{{x^2} - 1}}{{{x^4} - {x^2} + 1}} - \frac{{{x^2} + 3}}{{{x^4} + 4{x^2} + 3}}\).
a) Rút gọn M.
b) Tìm giá trị lớn nhất của M.
Câu 6:
Một trường có 30 học sinh giỏi toán 25 học sinh giỏi văn và 5 học sinh giỏi cả văn và toán nhà trường quyết định chọn một học sinh giỏi văn hoặc toán đi dự trại hè toàn quốc hỏi nhà trường có bao nhiêu cách để chọn?
Câu 7:
Một ô tô đi từ A lúc 8 giờ. Đến 9 giờ một ô tô khác cũng đi xe từ A. Xe thứ nhất đến B lúc 2 giờ chiều. Xe thứ hai đến B sớm hơn xe thứ nhất nửa giờ. Tính vận tốc mỗi xe biết rằng vận tốc xe thứ hai lớn hơn vận tốc xe thứ nhất là 20 km/h.
