Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lấy lần lượt các điểm P, Q sao cho AP = CQ. Từ điểm P vẽ PM song song với BC (M ∈ AB). Chứng minh tứ giác PCQM là hình chữ nhật.
Câu hỏi:
Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lấy lần lượt các điểm P, Q sao cho AP = CQ. Từ điểm P vẽ PM song song với BC (M ∈ AB). Chứng minh tứ giác PCQM là hình chữ nhật.
Trả lời:
Lời giải
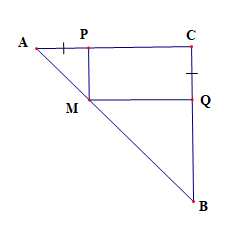
Vì tam giác ABC vuông cân tại C
Nên AC = BC, \(\widehat {CAB} = \widehat {CBA} = 45^\circ \)
Ta có PM // BC và AC ⊥ CB
Suy ra PM ⊥ AC
Do đó tam giác APM vuông tại P
Lại có \(\widehat {PAM} = 45^\circ \)
Suy ra \(\widehat {PAM} = \widehat {PMA} = 45^\circ \)
Do đó tam giác APM vuông cân tại P
Suy ra PA = PM
Mà PA = CQ (giả thiết)
Suy ra PM = CQ
Xét tứ giác PCQM có
PM = CQ
Mà PM // CQ
Suy ra PCQM là hình bình hành
Lại có: \(\widehat C = 90^\circ \)
Suy ra PCQM là hình chữ nhật
Vậy PCQM là hình chữ nhật.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho tam giác ABC vuông tại A có đường cao AH biết AC = 20 cm, BH = 9 cm. Tính BC và AH?
Xem lời giải »
Câu 2:
Cho hàm số (P): y = x2 – 3x + 2 và (d): y = x + m. Tìm M để (d) và (P) cắt nhau tại hai điểm phân biệt.
Xem lời giải »
Câu 3:
Tìm tập hợp các giá trị của tham số thực m để hàm số \(y = \sqrt {{x^2} + 1} - m{\rm{x}} - 1\) đồng biến trên ℝ
Xem lời giải »
Câu 4:
Cho hàm số y = (2m – 1)x + 3 – m có đồ thị (d). Xác định m để đường thẳng (d) song song với đồ thị hàm số y = 2x + 5.
Xem lời giải »
Câu 5:
Cho đoạn thẳng AB có O là trung điểm và cho điểm M tùy ý. Chứng minh rằng: \(\overrightarrow {MA} .\overrightarrow {MB} = M{O^2} - O{A^2}\).
Xem lời giải »
Câu 6:
Ảnh của đường tròn (C): x2 + y2 + 2y = 0 qua phép vị tự tâm O(0; 0) tỉ số k = –11 là đường tròn:
Xem lời giải »
Câu 7:
Chứng minh bất đẳng thức: \[{\rm{cosx > 1}} - \frac{{{x^2}}}{2}\] với mọi x ≠ 0.
Xem lời giải »
Câu 8:
Chứng minh định lí sau: Nếu trong tam giác vuông có 1 cạnh góc vuông bằng nửa cạnh huyền thì góc đối diện với cạnh ấy bằng 30°.
Xem lời giải »


