Cho tam giác ABC vuông ở A, đường cao AH. Kẻ HD vuông góc với AB và HE
Câu hỏi:
Cho tam giác ABC vuông ở A, đường cao AH. Kẻ HD vuông góc với AB và HE vuông góc với AC (D trên AB, E trên AC). Gọi O là giao điểm của AH và DE.
a) Chứng minh AH = DE.
b) Gọi P và Q lần lượt là trung điểm của BH và HC. Chứng minh tứ giác DEQP là hình thang vuông.
c) Chứng minh O là trực tâm của tam giác ABQ.
d) Chứng minh SABC = 2SDEQP.
Trả lời:
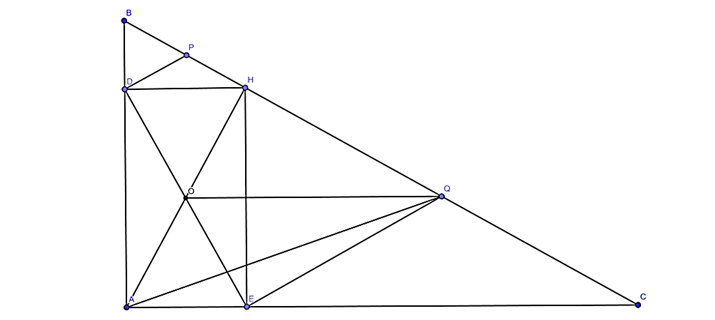
a) Xét tứ giác ADHE có 3 góc vuông (\(\widehat A,\widehat D,\widehat E\))
⇒ ADHE là hình chữ nhật mà AH, DE là 2 đường chéo
⇒ AH = DE (đpcm)
b) HD ⊥ AB và AC ⊥ AB ⇒ HD // AC
⇒ \(\widehat {PHD} = \widehat {HCA}\)(đồng vị)
ΔDBH vuông tại D có DP là trung tuyến ứng với cạnh huyền
⇒ DP = PH ⇒ ΔDPH cân tại P
⇒ \(\widehat {PHD} = \widehat {PDH}\)
ADHE là hình chữ nhật ⇒ \(\widehat {ADE} = \widehat {AHE}\)
mà \(\widehat {HCA} = \widehat {AHE}\) (cùng phụ với \(\widehat {HAE}\))
⇒ \(\widehat {ADE} = \widehat {HCA} = \widehat {PHD} = \widehat {PDH}\)
Ta có: \(\widehat {ADE} + \widehat {EDH} = 90^\circ \)
⇒ \(\widehat {PDH} + \widehat {EDH} = 90^\circ \)
⇒ \(\widehat {PDE} = 90^\circ \) ⇒ DP ⊥ DE
Chứng minh tương tự ta có EQ ⊥ DE
⇒ Tứ giác DEQP là hình thang vuông tại D và E (đpcm)
c) Xét ΔHAC có O là trung điểm của HA, Q là trung điểm của HC
⇒ OQ là đường trung bình ⇒ OQ // AC ⇒ OQ ⊥ AB
Xét ΔABQ có QO, AH là 2 đường cao cắt nhau tại O
⇒ O là trực tâm ΔABQ (đpcm)
d) SABC = \(\frac{1}{2}.AH.BC = PQ.AH\left( 1 \right)\)
SDEQP = \(\frac{1}{2}\left( {DP + EQ} \right).DE = \frac{1}{2}.\left( {DP + EQ} \right).AH = \frac{1}{2}.\left( {HP + HQ} \right).AH = \frac{1}{2}.PQ.AH\) (2)
Từ (1) và (2) suy ra: SABC = 2SDEQP (đpcm).

