Câu hỏi:
Cho tam giác ABC vuông tại A. Đặt BC = a, AC = b, AB = c, kẻ đường cao AH của tam giác ABC. Tính tỉ số \(\frac{{BH}}{{CH}}\) theo a, b, c.
Trả lời:
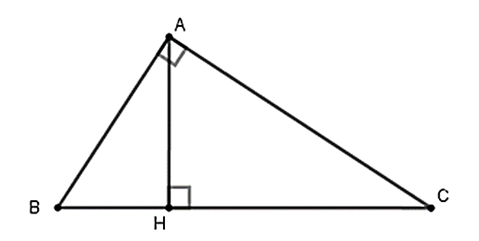
Áp dụng hệ thức lượng trong tam giác vuông ta dó:
AB2 = BH.BC hay c2 = BH.a
Suy ra: \(BH = \frac{{{c^2}}}{a}\)
AC2 = CH.BC suy ra: \(CH = \frac{{{b^2}}}{a}\)
\(\frac{{BH}}{{CH}} = \frac{{{c^2}}}{a}:\frac{{{b^2}}}{a} = \frac{{{c^2}}}{{{b^2}}}\).
Câu 1:
Cho hình bình hành ABCD. Chứng minh rằng \(\overrightarrow {AB} + 2\overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AC} \).
Câu 2:
Cho biểu thức \(A = 1 + \left( {\frac{{2a + \sqrt a - 1}}{{1 - a}} - \frac{{2a\sqrt a - \sqrt a + a}}{{1 - a\sqrt a }}} \right).\frac{{a - \sqrt a }}{{2\sqrt a - 1}}\). Rút gọn A.
Câu 4:
Rút gọn phân thức: \(\frac{{\left( {{x^2} + 3x + 2} \right)\left( {{x^2} - 25} \right)}}{{{x^2} + 7x + 10}}\).
Câu 8:
Cho tam giác ABC có AB = 6 cm, AC = 9 cm, BC = 10 cm, đường phân giác trong AD, đường phân giác ngoài AE.
a) Tính DB, EB.
b) Chứng minh tam giác ADE vuông.
c) Tính tỉ số diện tích của tam giác ABD và tam giác ADC.
