Cho tam giác ABC có AB = 6 cm, AC = 9 cm, BC = 10 cm, đường phân giác trong AD
Câu hỏi:
Cho tam giác ABC có AB = 6 cm, AC = 9 cm, BC = 10 cm, đường phân giác trong AD, đường phân giác ngoài AE.
a) Tính DB, EB.
b) Chứng minh tam giác ADE vuông.
c) Tính tỉ số diện tích của tam giác ABD và tam giác ADC.
Trả lời:
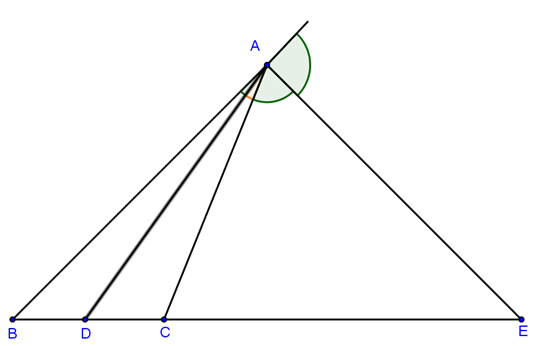
a) Theo tính chất đường phân giác ta có:
\(\frac{{DB}}{{AB}} = \frac{{DC}}{{AC}} = \frac{{DB + DC}}{{AB + AC}} = \frac{{BC}}{{AB + AC}} = \frac{{10}}{{15}} = \frac{2}{3}\)
Suy ra: DB = \(\frac{2}{3}AB = \frac{2}{3}.6 = 4\left( {cm} \right)\)
\(\frac{{EB}}{{AB}} = \frac{{EC}}{{AC}} = \frac{{EC - EB}}{{AC - AB}} = \frac{{BC}}{{AC - AB}} = \frac{{10}}{{9 - 6}} = \frac{{10}}{3}\)
⇒ EB = \(\frac{{10}}{3}.6 = 20\left( {cm} \right)\)
b) Vì AE và AD là phân giác của 2 góc kề bù
⇒ \(\widehat {EAD}\)vuông
⇒ Tam giác ADE vuông tại A
c) Ta có tam giác ABD và ADC có chung đường cao hạ từ đỉnh A nên tỉ số diện tích 2 tam giác chính là tỉ số giữa 2 cạnh đáy
Mà theo tính chất đường phân giác: \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\)
⇒ \(\frac{{{S_{ABD}}}}{{{S_{ADC}}}} = \frac{{DB}}{{DC}} = \frac{{AB}}{{AC}} = \frac{6}{9} = \frac{2}{3}\)
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hình bình hành ABCD. Chứng minh rằng \(\overrightarrow {AB} + 2\overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AC} \).
Xem lời giải »
Câu 2:
Cho biểu thức \(A = 1 + \left( {\frac{{2a + \sqrt a - 1}}{{1 - a}} - \frac{{2a\sqrt a - \sqrt a + a}}{{1 - a\sqrt a }}} \right).\frac{{a - \sqrt a }}{{2\sqrt a - 1}}\). Rút gọn A.
Xem lời giải »
Câu 4:
Rút gọn phân thức: \(\frac{{\left( {{x^2} + 3x + 2} \right)\left( {{x^2} - 25} \right)}}{{{x^2} + 7x + 10}}\).
Xem lời giải »
Câu 5:
Cho hình thang vuông ABCD có AB = BC = a, AD = 2a. Chứng minh AC vuông góc DC.
Xem lời giải »
Câu 6:
Cho tam giác ABC có AB = 1, \(\widehat A = 105^\circ ,\widehat B = 60^\circ \). Trên cạnh BC lấy điểm E sao cho BE = 1. Vẽ ED song song với AB. Chứng minh: \(\frac{1}{{A{C^2}}} + \frac{1}{{A{D^2}}} = \frac{4}{3}\).
Xem lời giải »
Câu 7:
Cho tam giác vuông ABC có \(\widehat A = 90^\circ \). Kết quả nào sau đây đúng?
Xem lời giải »
Câu 8:
Cho định lí: "Nếu m,n là hai số nguyên dương và mỗi số đều chia hết cho 3 thì m2 + n2 cũng chia hết cho 3". Hãy phát biểu và chứng định lí đảo của định lí trên (nếu có).
Xem lời giải »


