Hàm số y = 3f(x + 2) - x^3 + 3x đồng biến trên khoảng nào dưới đây

Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau:

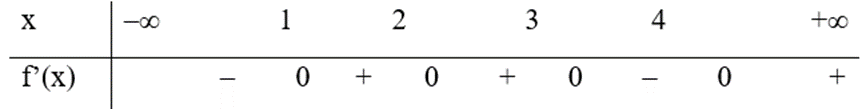
Hàm số y = 3f(x + 2) – x³ + 3x đồng biến trên khoảng nào dưới đây?

A. (1; +∞)

B. (–∞; –1)

C. (–1; 0)

D. (0; 2).

Đáp án đúng là: C

Ta có: y’ > 0 ⇔ 3f’(x + 2) – 3x² + 3 > 0

⇔ 3f’(x + 2) > 3x² – 3

⇔ f’(x + 2) > x² – 1

Đặt t = x + 2, suy ra x = t – 2.

Khi đó f’(t) > (t – 2)² – 1

Chọn t sao cho \(\left\{ \begin{array}{l}{\left( {t - 2} \right)^2} - 1 < 0\\f'\left( t \right) > 0\end{array} \right.\)           

\( \Leftrightarrow \left\{ \begin{array}{l} - 1 < t - 2 < 1\\t \in \left( {1;2} \right) \cup \left( {2;3} \right) \cup \left( {4; + \infty } \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 < t < 3\\t \in \left( {1;2} \right) \cup \left( {2;3} \right) \cup \left( {4; + \infty } \right)\end{array} \right.\)

\( \Leftrightarrow \left[ \begin{array}{l}1 < t < 2\\2 < t < 3\end{array} \right. \Rightarrow \left[ \begin{array}{l}1 < x + 2 < 2\\2 < x + 2 < 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l} - 1 < x < 0\\0 < x < 1\end{array} \right.\)

Suy ra hàm số đã cho đồng biến trên khoảng (–1; 0) và (0; 1).

Vậy ta chọn đáp án C.