Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi I là trung điểm của AB
Câu hỏi:
Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi I là trung điểm của AB và D là điểm đối xứng của M qua I.
a. Chứng minh: AD//BM và tứ giác ADBM là hình thoi.
b. Gọi E là giao điểm AM và DC. Chứng minh: AE = EM.
Trả lời:
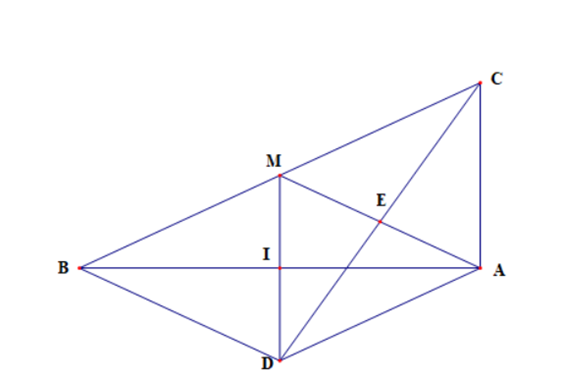
a) Xét tứ giác ADBM có I là trung điểm của hai đường chéo MD và AB
Suy ra ADBM là hình bình hành
Lại có AB ⊥ MD (do D là điểm đối xứng của M qua I)
Do đó ADBM là hình thoi
Suy ra AD // BM
b) Vì ADBM là hình thoi nên AM // BD
Ta có: CA ⊥ AB và MI ⊥ AB
Suy ra CA // MI (quan hệ từ vuông góc đến song song)
Xét tứ giác ADMC có CM // AD, MD // AC
Suy ra ADMC là hình bình hành
Mà AM cắt CD tại trung điểm E nên AE = EM
Vậy AE = EM.

