Hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc mặt phẳng đáy
Câu hỏi:
Hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc mặt phẳng đáy, SA = \(a\sqrt 6 \). Tính góc giữa SC và (SAB).
Trả lời:
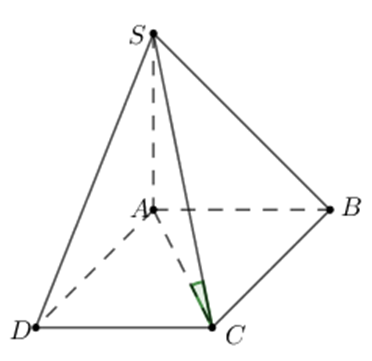
Ta có: \[\left\{ \begin{array}{l}CB \bot AB\\CB \bot SA\end{array} \right.\]
Suy ra: CB ⊥ (SAB)
Hay B là hình chiếu của C lên (SAB)
Suy ra: (SC,(SAB) = (SC,SB) = \(\widehat {CSB}\)
Xét tam giác SBC vuông tại B có BC = a, SB = \(\sqrt {A{B^2} + S{A^2}} = a\sqrt 7 \)
tan\(\widehat {CSB} = \frac{{BC}}{{SB}} = \frac{a}{{a\sqrt 7 }} = \frac{1}{{\sqrt 7 }}\)
⇒ \(\widehat {CSB} = \arctan \frac{1}{{\sqrt 7 }} \approx 20,7^\circ \).

