Cho tam giác MNP vuông tại M đường cao MH. Gọi D, F lần lượt là chân các đường
Câu hỏi:
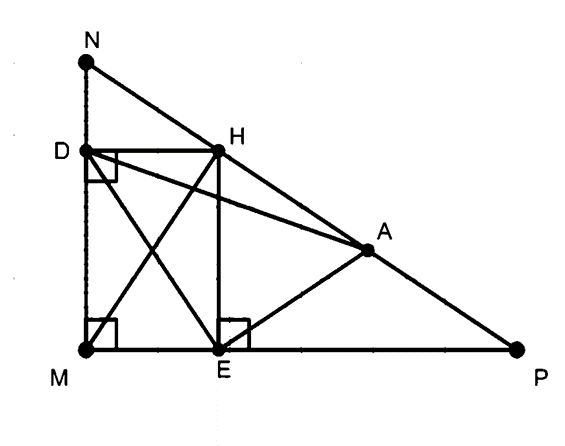
Cho tam giác MNP vuông tại M đường cao MH. Gọi D, F lần lượt là chân các đường vuông góc HA từ H xuống MN và MP.
a) Chứng minh tứ giác MDHE là Hình chữ nhật.
b) Gọi A là trung điểm HP. Chứng minh ∆DEA là tam giác vuông.
c) Tam giác MNP có thêm điều kiện gì để DE = 2EA.
Trả lời:
a) Tứ giác MDHE có \(\widehat M = \widehat D = \widehat E = 90^\circ \)
Vậy tứ giác MDHE là hình chữ nhật vì có 3 góc vuông.
b) Ta có: \(\widehat {DEH} = \widehat {MHE}\) (do MDHE là hình chữ nhật)
\(\widehat {HEA} = \widehat {EHA}\) (dễ dàng chứng minh được △HEA cân tại A nhờ giả thiết A trung điểm HP và HE⊥MP)
Mà \(\widehat {MHE} + \widehat {EHA} = 90^\circ \)nên \(\widehat {DEH} + \widehat {HEA} = \widehat {DEA} = 90^\circ \).
⇒ Tam giác DEA vuông tại E.
c) Ta có: DE = MH
2EA = HP
Để DE = 2EA thì MH = HP
⇔ Tam giác MHP cân tại H
⇔ Tam giác MHP vuông cân tại H
⇔ \(\widehat P = 45^\circ \)
⇔ Tam giác MNP vuông cân tại M.