Cho tứ diện ABCD. Gọi P, Q lần lượt là trung điểm của AB, CD. Điểm R nằm trên cạnh BC sao cho BR = 2RC. Gọi S là giao điểm của mp (PQR) và AD. Khi đó: A. SA = 3SD. B. SA = 2SD. C. SA = SD.
Câu hỏi:
Cho tứ diện ABCD. Gọi P, Q lần lượt là trung điểm của AB, CD. Điểm R nằm trên cạnh BC sao cho BR = 2RC. Gọi S là giao điểm của mp (PQR) và AD. Khi đó:
A. SA = 3SD.
B. SA = 2SD.
C. SA = SD.
D. 2SA = 3SD.
Trả lời:
Lời giải
Đáp án đúng là: B
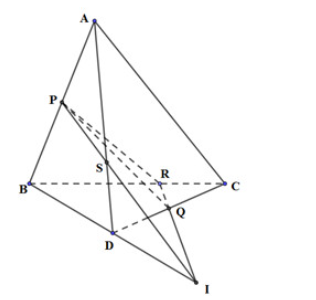
Trong (BCD) gọi I là giao điểm của RQ và BD
Trong (ABD) gọi S là giao điểm của AD và IP
Khi đó, S = AD ∩ (PQR)
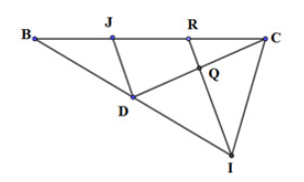
Gọi J là trung điểm của BR. DO R nằm trên cạnh BC sao cho BR = 2RC
Suy ra BJ = JR = RC
Xét tam giác JCD có R, Q lần lượt là trung điểm của JC, CD
Suy ra RQ là đường trung bình
Do đó RQ // JD, hay RI // JD
Xét tam giác BRI có J là trung điểm của BR và DJ // RI
Suy ra D là trung điểm của BI
Xét tam giác ABI có P, D lần lượt là trung điểm của AD, BI và PI cắt AD tại S
Suy ra S là trọng tâm tam giác ABI
Do đó SA = 2SD
Vậy ta chọn đáp án B.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho tam giác ABC cân tại A nội tiếp đường tròn tâm O. Gọi D là trung điểm của AB, E là trọng tâm tam giác ACD. Chứng minh rằng OE vuông góc với CD.
Xem lời giải »
Câu 2:
Cho hình vuông ABCD cạnh bằng 2. Điểm M nằm trên đoạn thẳng AC sao cho \[{\rm{A}}M = \frac{{AC}}{4}\]. Gọi N là trung điểm của đoạn thẳng DC. Tính \(\overrightarrow {MB} .\overrightarrow {MN} \).
Xem lời giải »
Câu 3:
Cho hình vuông ABCD có cạnh bằng 2. Tính \(T = \left| {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {A{\rm{D}}} } \right|\).
Xem lời giải »
Câu 4:
Cho tam giác ABC cân tại A, O là trung điểm của BC. Vẽ đường tròn tâm O tiếp xúc với AB, AC tại H và K. Lấy E bất kỳ thuộc cung nhỏ HK. Vẽ tiếp tuyến tại E cắt AB, AC ở M, N.
a) Giả sử \(\widehat B = \widehat C = \alpha \). Tính \(\widehat {MON}\).
b) Chứng minh rằng OM, ON chia tứ giác BMNC thành ba tam giác đồng dạng.
c) Giả sử BC = 2a. Tính BM . CN.
d) MN ở vị trí nào thì tổng BM + CN nhỏ nhất?
Xem lời giải »
Câu 5:
Cho một hình trụ có bán kính đáy bằng R và có chiều cao bằng \(R\sqrt 3 \). Hai điểm A, B lần lượt nằm trên hai đường trong đáy sao cho góc giữa AB và trục của hình trụ bằng 30°. Khoảng cách giữa AB và trục của hình trụ bằng:
Xem lời giải »
Câu 6:
Một người gửi ngân hàng 100 triệu đồng với kỳ hạn 3 tháng, lãi suất 2% một quý theo hình thức lãi kép. Sau đúng 6 tháng, người đó gửi thêm 100 triệu đồng với kỳ hạn và lãi suất như trước đó. Tổng số tiền người đó nhận được sau 1 năm kể từ khi bắt đầu gửi tiền gần với kết quả nào sau đây:
Xem lời giải »
Câu 7:
Cho tam giác ABC vuông tại A có AB = 8 cm, AC = 6 cm, trung tuyến AM. Kẻ MD vuông góc với AB và Me vuông góc với AC.
a) Tứ giác ADME là hình gì? Vì sao?
b) Tìm điều kiện của tam giác ABC để tứ giác ADME là hình vuông.
c) Tính độ dài AM?
d) Tính diện tích tam giác ABM?
Xem lời giải »
Câu 8:
Cho tam giác ABC vuông tại A. Gọi D và E lần lượt là trung điểm của AB và BC.
a) Chứng minh tứ giác ACED là hình thang vuông.
b) Gọi F là điểm đối xứng của E qua D. Chứng minh ACEF là hình bình hành.
c) Chứng minh AEBF là hình thoi.
Xem lời giải »



