Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng M, N, P, Q cùng nằm trên một đường tròn.
Câu hỏi:
Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng M, N, P, Q cùng nằm trên một đường tròn.
Trả lời:
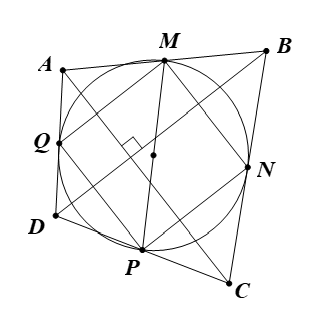
Ta có MN, NP, PQ, QM lần lượt là đường trung bình của các tam giác ABC, BCD, ACD, ABD.
Suy ra MN // AC; NP // BD; PQ // AC; QM // BD.
Mà AC ⊥ BD (giả thiết).
Do đó MN ⊥ NP và PQ ⊥ QM.
Vì vậy .
Suy ra tứ giác MNPQ nội tiếp đường tròn đường kính MP.
Vậy M, N, P, Q cùng nằm trên một đường tròn.

