Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AD, BC a) Chứng minh: vec tơ MN =1/2 ( vec tơ AB + CD)

❮ Bài trước Bài sau ❯

Câu hỏi:

Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AD, BC

a) Chứng minh: $\vec{M N} = \frac{1}{2} (\vec{A B} + \vec{D C})$

b) Xác định điểm O sao cho $\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} = \vec{0}$ .

Trả lời:

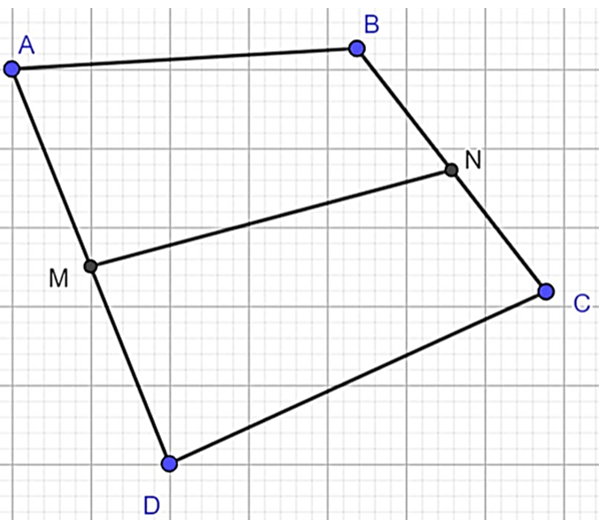
Media VietJack

a) $\vec{M N} = \vec{M A} + \vec{A B} + \vec{B N}$

$\vec{M N} = \vec{M D} + \vec{D C} + \vec{C N}$

$\Rightarrow 2 \vec{M N} = (\vec{M A} + \vec{M D}) + \vec{A B} + \vec{D C} + (\vec{B N} + \vec{C N})$

$\Rightarrow 2 \vec{M N} = \vec{0} + \vec{A B} + \vec{D C} + \vec{0}$

$\Rightarrow \vec{M N} = \frac{1}{2} (\vec{A B} + \vec{D C})$

b) $\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} = \vec{0}$

$\Leftrightarrow \vec{O A} + \vec{O D} + \vec{O B} + \vec{O C} = \vec{0}$

$\Leftrightarrow 2 \vec{O M} + 2 \vec{O N} = \vec{0}$

$\Leftrightarrow 2 (\vec{O M} + \vec{O N}) = \vec{0}$

$\Leftrightarrow 2 . 2 \vec{O I} = \vec{0}$ (Với I là trung điểm của MN)

\Leftrightarrow 4 . \vec{O I} = \vec{0}

\Leftrightarrow \vec{O I} = \vec{0}

Suy ra O º I.

Vậy O là trung điểm của MN.

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Tính giá trị lớn nhất của hàm số y = x(2 − ln x) trên đoạn [2; 3].

Xem lời giải »

Câu 2:

Tìm giá trị nhỏ nhất của hàm số y = x²ln x trên đoạn [1; 2].

Xem lời giải »

Câu 3:

Hàm số y = cos 2x đồng biến trên khoảng nào?

Xem lời giải »

Câu 4:

Hàm số y = cos 2x nghịch biến trên khoảng nào sau đây (k Î ℤ).

Xem lời giải »

Câu 5:

Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của DA, BC. Tính góc giữa hai đường thẳng AB và CD biết

A B = C D = 2 a; M N = a \sqrt{3}

Xem lời giải »

Câu 6:

Cho hình chóp tam giác đều S.ABC có đáy bằng 3a, góc giữa cạnh bên và mặt đáy bằng 45°. Thể tích khối cầu ngoại tiếp hình chóp S.ABC bằng:

Xem lời giải »

Câu 7:

Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, góc giữa cạnh bên và mặt đáy bằng 60°. Tính thể tích V của khối chóp.

Xem lời giải »

Câu 8:

Lãi suất gửi tiết kiệm của ngân hàng A thời gian vừa qua thay đổi liên tục. Bạn Duy gửi số tiền ban đầu là 10 triệu đồng với lãi suất 0,8% một tháng. Chưa đầy một năm, thì lãi suất tăng lên 1,2% một tháng trong nửa năm tiếp theo. Và bạn Duy tiếp tục gửi; sau nửa năm đó lãi suất giảm xuống còn 1% một tháng. Đồng thời bạn Duy quyết định gửi thêm một số tháng tròn nữa. Biết rằng khi rút tiền bạn Duy được cả vốn lẫn lãi là 12 153 337,95 triệu đồng. Tổng số tháng mà bạn Duy gửi tiết kiệm là:

Xem lời giải »

❮ Bài trước Bài sau ❯

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án

Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AD, BC a) Chứng minh: vec tơ MN =1/2 ( vec tơ AB + CD)

Xem thêm bài tập Toán có lời giải hay khác: