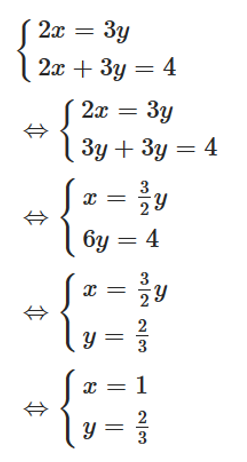Cho $A=\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\mathrm{...}+\frac{1}{2017}$  và $B=\frac{1}{2016}+\frac{2}{2015}+\frac{3}{2014}+\mathrm{...}+\frac{2015}{2}+\frac{2016}{1}$

. Tính $\frac{B}{A}.$

Biết 36 l dầu cân nặng 27kg. Một can chứa dầu cân nặng tất cả 10,5 kg. Hỏi trong can đó chứa bao nhiêu lít dầu, biết rằng cái can rỗng cân nặng 1,5 kg?

Lãi suất tiết kiệm là 0,65% một tháng. Hỏi người ta phải gửi bao nhiêu tiền để sau một tháng được tiền lãi là 104 000 đồng?

Từ 1 điểm A nằm ngoài đường tròn (O; R), kẻ 2 tiếp tuyến AB, AC
với (O; R) (B và C là 2 tiếp điểm).

a) Chứng minh 4 điểm A, B, O, C cùng thuộc 1 đường tròn và AO ⊥ BC tại H.

Tổng của tất cả các số lẻ có 2 chữ số giống nhau được gấp lên 9 lần thì được kết quả bao nhiêu?

Viết số thích hợp vào chỗ chấm : 627m² = ... ha?

Một bếp ăn chuẩn bị số gạo cho 36 người ăn trong 50 ngày. Nhưng thực tế có 60 người ăn, hỏi số gạo đã chuẩn bị đủ dùng trong bao nhiêu ngày? (Mức ăn của mỗi người như nhau).