Cho x, y là hai số thực thỏa mãn điều kiện . Tìm giá trị lớn nhất
Câu hỏi:
Cho x, y là hai số thực thỏa mãn điều kiện . Tìm giá trị lớn nhất của biểu thức
A. 100
B. 66
C. 110
D. 90
Trả lời:
Lời giải:
Theo giả thiết:
Ta xem đây là phương trình bậc hai ẩn y và khi đó điều kiện có nghiệm là:
Từ giả thiết suy ra . Khi đó:
Đặt (ta xem x là tham số)
Khi đó
Do nên
Suy ra . Vậy giá trị lớn nhất của P là 100 khi
Đáp án cần chọn là: A
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hàm số liên tục trên R và có đồ thị như hình dưới. Gọi a, A lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của trên đoạn . Giá trị bằng:
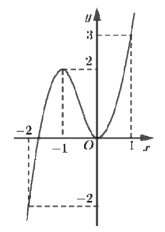
Xem lời giải »
Câu 2:
Cho hàm số liên tục trên đoạn và có đồ thị như hình vẽ:

Có tất cả bao nhiêu giá trị nguyên của m thuộc đoạn để bất phương trình đúng với mọi x thuộc đoạn ?
Xem lời giải »
Câu 3:
Gọi M, N lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn . Tính
Xem lời giải »
Câu 4:
Tìm giá trị lớn nhất của hàm số trên đoạn
Xem lời giải »
Câu 6:
Cho hàm số . Gọi M là giá trị lớn nhất của hàm số trên đoạn . Tổng các giá trị của tham số thực m để
Xem lời giải »

