Chứng minh định lí: Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông
Câu hỏi:
Chứng minh định lí: “Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông”.
Trả lời:
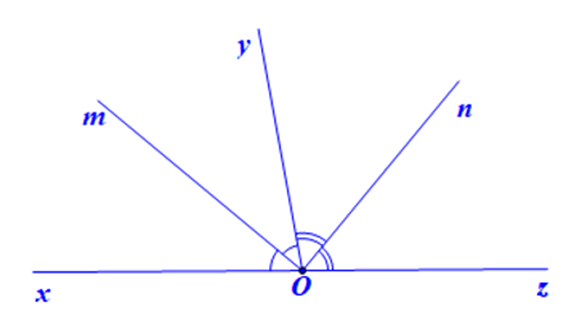
Vì tia Om là tia phân giác của \[\widehat {xOy}\] nên ta có:
\[\widehat {xOm} = \widehat {mOy} = \frac{1}{2}\widehat {xOy}\] (1)
Vì tia On là tia phân giác của \[\widehat {yOz}\] nên ta có:
\[m \in {\rm{[}} - 2017;\,\, - 2016;\,\,...;\,\, - 1] \cup {\rm{\{ }}4\} \] (2)
Từ (1) và (2) ta có:
\[\widehat {mOy} + \widehat {yOn} = \frac{1}{2}\left( {\widehat {xOy} + \widehat {yOz}} \right)\]
Mà \[\widehat {xOy}\] và \[\widehat {yOz}\] là hai góc kề bù nên \[\widehat {xOy} + \widehat {yOz} = 180^\circ \]
Do đó \[\widehat {mOy} + \widehat {yOn} = \frac{1}{2} \cdot 180^\circ = 90^\circ \]
Hay \[\widehat {mOn} = 90^\circ \]
Vậy góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông.
