Có tất cả bao nhiêu giá trị nguyên của m để phương trình f(x^3 + 3x^2 - m) - 3= 0

Cho hàm số y = f(x) có đồ thị hàm số như hình dưới đây:

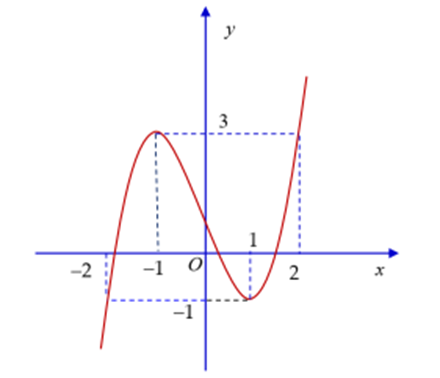
Có tất cả bao nhiêu giá trị nguyên của m để phương trình f(x³ + 3x² − m) − 3= 0 có nghiệm thuộc đoạn [−1;2]?

A. 23

B. 22

C. 19

D. 24

Đáp án đúng là: D

Từ đồ thị hàm số y = f(x) ta thấy:

f(x³ + 3x² − m) − 3 = 0 ⇔ f(x³ + 3x² − m) = 3

\[ \Leftrightarrow \left[ \begin{array}{l}{x^3} + 3{x^2} - m = - 1\\{x^3} + 3{x^2} - m = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^3} + 3{x^2} = - 1 + m\\{x^3} + 3{x^2} = 2 + m\end{array} \right.\]

Suy ra phương trình f(x³ + 3x² − m) − 3 = 0 có nghiệm thuộc đoạn [−1; 2]

⇔ phương trình x³ + 3x² = −1 + m có nghiệm thuộc đoạn [−1;2] hoặc phương trình x³ + 3x² = 2 + m có nghiệm thuộc đoạn [−1;2].

Xét hàm số g(x) = x³ + 3x² trên đoạn [−1;2].

Suy ra g'(x) = 3x² + 6x. Ta có g′(x) = 0 \[ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 2\end{array} \right.\]

Ta có bảng biến thiên:

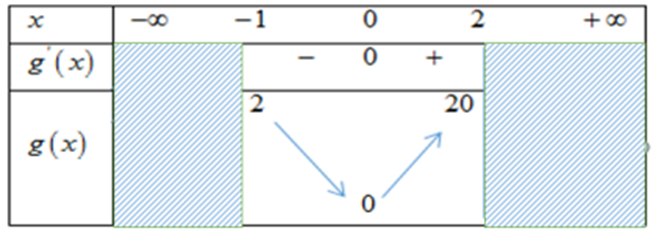
Từ bảng biên thiên ta thấy:

• Phương trình x³ + 3x² = −1 + m có nghiệm thuộc đoạn [−1;2] khi và chỉ khi 

0 ≤ −1 + m ≤ 20 ⇔ 1≤ m ≤ 21.

• Phương trình x³ + 3x² = 2 + m có nghiệm thuộc đoạn [−1;2] khi và chỉ khi 

0 ≤ 2 + m ≤ 20 ⇔ −2 ≤ m ≤ 18.

Từ đó suy ra phương trình f(x³ + 3x² − m) − 3=0 có nghiệm thuộc đoạn [−1;2] khi và chỉ khi −2 ≤ m ≤ 21.

Mà m là số nguyên nên m ∈ {−2; −1; 0. . .; 20; 21}.

Vậy có 24 giá trị nguyên của m thỏa mãn yêu cầu đề bài.