Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức
Câu hỏi:
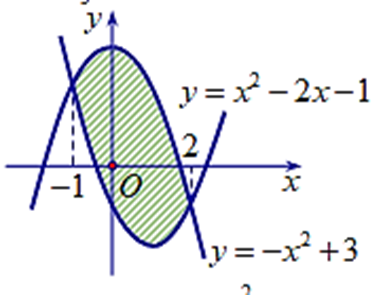
Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?
A. \(\int\limits_{ - 1}^2 {\left( {2{x^2} - 2x - 4} \right)dx} \);
B. \(\int\limits_{ - 1}^2 {\left( { - 2x + 2} \right)dx} \);
C. \(\int\limits_{ - 1}^2 {\left( {2x - 2} \right)dx} \);
D. \(\int\limits_{ - 1}^2 {\left( { - 2{x^2} + 2x + 4} \right)dx} \).
Trả lời:
Đáp án đúng là: D
Ta thấy "x Î [−1; 2]: −x2 + 3 ≥ x2 − 2x − 1 nên
\(S = \int\limits_{ - 1}^2 {\left[ {\left( { - {x^2} + 3} \right) - \left( {{x^2} - 2x - 1} \right)} \right]dx} = \int\limits_{ - 1}^2 {\left( { - 2{x^2} + 2x + 4} \right)dx} \).

