Đường tròn nội tiếp hình vuông cạnh a có bán kính là: A. a căn bậc hai 2 B. a
Câu hỏi:
Đường tròn nội tiếp hình vuông cạnh a có bán kính là:
A. \[a\sqrt 2 .\]
B. \[\frac{{a\sqrt 2 }}{2}.\]
C. \[\frac{a}{2}.\]
D. \[\frac{{a\sqrt 3 }}{2}.\]
Trả lời:
Đáp án đúng là: C
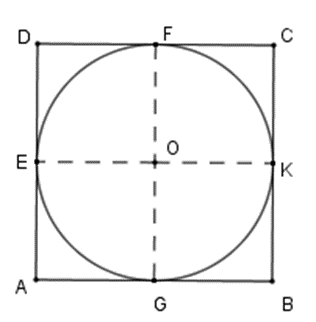
Gọi O là tâm của hình vuông ABCD; E, F, K, G là trung điểm của AD, DC, BC, AB
Khi đó ta có \[OE = OF = OK = OG = \frac{a}{2}.\] Hay O là tâm đường tròn nội tiếp hình vuông ABCD
Bán kính đường tròn là \[R = \frac{a}{2}.\]

