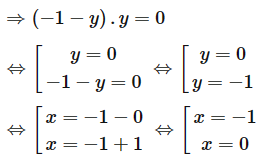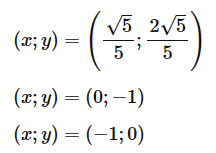Giải hệ phương trình: x^2 + x - xy - 2y^2}- 2y = 0; x^2 + y^2 = 1
Câu hỏi:
Giải hệ phương trình: \(\left\{ \begin{array}{l}{x^2} + x - xy - 2{y^2} - 2y = 0\\{x^2} + {y^2} = 1\end{array} \right.\).
Trả lời:
Lời giải
Ta có:
\({x^2} + x - xy - 2{y^2} - 2xy = 0\)
\( \Leftrightarrow {x^2} - 2xy + xy - 2{y^2} + x - 2y = 0\)
\( \Leftrightarrow x(x - 2y) + y(x - 2y) + (x - 2y) = 0\)
\( \Leftrightarrow (x + y + 1)(x - 2y) = 0\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x + y + 1 = 0}\\{x - 2y = 0}\end{array}} \right.\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x + y = - 1}\\{x = 2y}\end{array}} \right.\)
Thay x = 2y vào phương trình x2 + y2 = 1 ta có:
\(4{y^2} + {y^2} = 1\)
\( \Leftrightarrow 5{y^2} = 1\)
\( \Leftrightarrow {y^2} = \frac{1}{5}\)
\( \Leftrightarrow y = \frac{{\sqrt 5 }}{5}\)
\( \Rightarrow x = 2 \cdot \frac{{\sqrt 5 }}{5} = \frac{{2\sqrt 5 }}{5}\)
Ta có \(x + y = - 1\)
\( \Leftrightarrow {(x + y)^2} - 2xy = 1\)
\( \Leftrightarrow 1 - 2xy = 1\)
\( \Leftrightarrow xy = 0\)
Lại có x + y = –1
Do đó x = –1 – y
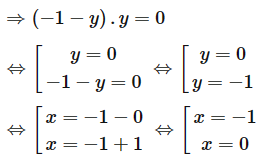
Vậy nghiệm của hệ phương trình là:
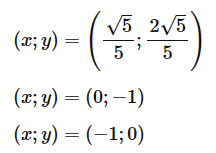
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho tam giác ABC vuông tại A có đường cao AH biết AC = 20 cm, BH = 9 cm. Tính BC và AH?
Xem lời giải »
Câu 2:
Cho hàm số (P): y = x2 – 3x + 2 và (d): y = x + m. Tìm M để (d) và (P) cắt nhau tại hai điểm phân biệt.
Xem lời giải »
Câu 3:
Tìm tập hợp các giá trị của tham số thực m để hàm số \(y = \sqrt {{x^2} + 1} - m{\rm{x}} - 1\) đồng biến trên ℝ
Xem lời giải »
Câu 4:
Cho hàm số y = (2m – 1)x + 3 – m có đồ thị (d). Xác định m để đường thẳng (d) song song với đồ thị hàm số y = 2x + 5.
Xem lời giải »
Câu 5:
Phân tích đa thức thành nhân tử x2 – x – xy – 2y2 + 2y.
Xem lời giải »
Câu 6:
Các nhà toán học đã xấp xỉ số π bởi số \(\frac{{355}}{{113}}\). Hãy đánh giá sai số tuyệt đối biết 3,14159265 < π < 3,14159266.
Xem lời giải »
Câu 7:
Cho điểm O ở ngoài mặt phẳng (α). Trong mặt phẳng (α) có đường thẳng d di động qua điểm A cố định. Gọi H, M lần lượt là hình chiếu của O trên mặt phẳng (α) và đường thẳng d. Độ dài đoạn OM lớn nhất khi
Xem lời giải »