Gọi G là trọng tâm của tam giac ABC. Từ G kẻ các đường thẳng song song với hai
Câu hỏi:
Gọi G là trọng tâm của tam giac ABC. Từ G kẻ các đường thẳng song song với hai cạnh AB và AC, cắt BC lần lượt tại D và E. So sánh ba đoạn thẳng BD, DE, EC.
Trả lời:
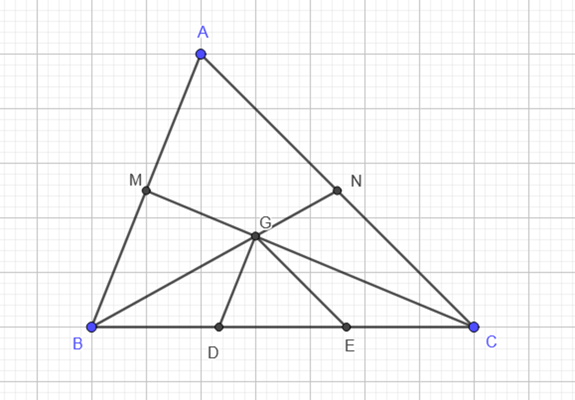
Gọi M là trung điểm của AB, N là trung điểm của AC
⇒ G = BN ∩ CM là trọng tâm của ΔABC
⇒ \(\frac{{CG}}{{CM}} = \frac{{BG}}{{BN}} = \frac{2}{3}\)
Do GD // AB theo Talet ta có:
\(\frac{{CD}}{{CB}} = \frac{{CG}}{{CM}} = \frac{2}{3}\)
⇒ \(\frac{{CB - CD}}{{CB}} = \frac{{3 - 2}}{3} = \frac{1}{3}\)
⇒ \(\frac{{DB}}{{CB}} = \frac{1}{3}\) ⇒ \(DB = \frac{1}{3}CB\)
Tương tự: GE // AC ⇒ \(\frac{{EC}}{{BC}} = \frac{1}{3}\)⇒ \(EC = \frac{1}{3}CB\)
⇒ DE = BC – DB – EC = BC – \( - \frac{1}{3}CB - \frac{1}{3}CB = \frac{1}{3}CB\)
Vậy DB = DE = EC = \( = \frac{1}{3}CB\).

