W1llyK!m#5991
Câu hỏi:
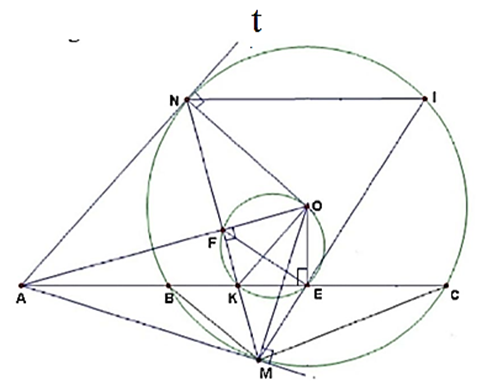
Cho A, B, C nằm trên đường thẳng xy theo thứ tự đó. Vẽ đường tròn (O) đi qua B và C. Từ điểm A, vẽ hai tiếp tuyến AM; AN. Gọi E và F lần lượt là trung điểm của BC và MN.
a) Chứng minh AM2 = AN2 = AB.AC.
b) ME cắt (O) tại I. Chứng minh IN // AB.
c) Chứng minh tâm đường tròn ngoại tiếp tam giác OEF nằm trên 1 đường thẳng cố định khi (O) thay đổi nhưng luôn đi qua B và C.
Trả lời:
a) Ta có AM và AN là hai tiếp tuyến cắt nhau
Nên AM = AN
Lại có: ABC là cát tuyến của (O)
Nên AM2 = AN2 = AB.AC
b) Dễ thấy OA vuông góc với MN tại trung điểm MN
⇒ OA vuông góc với MN tại F
Ta có \(\widehat {OMA} = \widehat {ONA} = \widehat {OEA} = \) 90°.
⇒ M, N, E đều thuộc đường tròn đường kính OA
⇒ EMAB nội tiếp
⇒ \(\widehat {EMN} = \widehat {EAN}\)(1)
Gọi Nt là tia đối của tia AN
Ta có (vì Nt là tiếp tuyến) (2)
Từ (1) và (2)
⇒ \(\widehat {EAN} = \widehat {INt}\)
⇒ IN//AE hay IN//AB
c) Gọi K là giao điểm của BC với MN
Ta có tứ giác OFKE nội tiếp trong đường tròn đường kính OK
Xét ∆AOE và ∆AFK có:
Chung \(\widehat A\)
\(\widehat {AFK} = \widehat {AEO} = 90^\circ \)
⇒ ∆AOE ∽ ∆AKF (g.g)
⇒ \(\frac{{AO}}{{AK}} = \frac{{AE}}{{AF}}\)
Suy ra: AK.AE = AF.AO
Mà AF.AO = AM2 = AB.AC
Suy ra: AK.AE = AB.AC không đổi
Vì AK không đổi nên K cố định
Vậy tâm đường tròn ngoại tiếp tam giác OEF là trung điểm của OK cố định.

