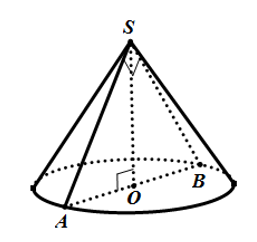
Thiết diện qua trục của một hình nón là một tam giác vuông cân có cạnh huyền bằng 2 căn 3 Thể tích của khối nón này là

Tìm tất cả các giá trị thực của tham số m để hàm số y = x³ – 3mx² – 9m²x nghịch biến trên khoảng (0; 1).

Điền từ thích hợp vào chỗ trống: Hai điểm M, N gọi là đối xứng nhau qua điểm I nếu .....

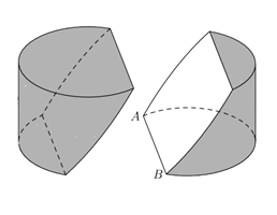
Một khối gỗ có hình trụ với bán kính đáy bằng 6 và chiều cao bằng 8. Trên một đường tròn đáy nào đó ta lấy hai điểm A, B sao cho cung AB có số đo bằng  $120°.$ Người ta cắt khúc gỗ bởi một mặt phẳng đi qua A, B và tâm của hình trụ (tâm của hình trụ là trung điểm của đoạn nối tâm hai đáy) để được thiết diện như hình vẽ. Tính diện tích S của thiết diện thu được.

Cho hai tam giác ABC và  A'B'C' lần lượt có trọng tâm là G và G' Đẳng thức nào sau đây là sai?

Cho hình nón có thiết diện qua đỉnh S tạo với đáy một góc  $60°$ là tam giác đều cạnh bằng 4. Thể tích của khối nón đó là:

Cho tập hợp A = [-1; 3], B = [m; m + 5]. Tìm m để A giao B bằng rỗng.

Cho nửa đường tròn tâm O, đường kính AB và dây cung CD không song song với AB. Gọi H và K là hình chiếu của A và B trên CD. Gọi E là giao điểm của BK với nửa đường tròn (O) và I là trung điểm của CD.

a) Chứng minh OI ⊥ AE.