Tìm các giá trị của tham số m để đồ thị hàm số y=x^4-2mx^2+2m+m^4

Câu hỏi:

Tìm các giá trị của tham số m để đồ thị hàm số: $y = x^{4} - 2 m x^{2} + 2 m + m^{4}$ có ba điểm cực trị là ba đỉnh của một tam giác đều

A. Không tồn tại m

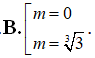
C. $m = \sqrt[3]{3}$ .

D. $m = \pm \sqrt{3}$ .

Trả lời:

Chọn C

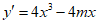
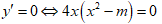
Hàm số có 3 cực trị $\Leftrightarrow m > 0$

Khi đó 3 điểm cực trị của đồ thị hàm số là

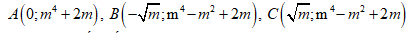
Do tính chất đối xứng, ta có $∆ A B C$ cân tại đỉnh A

Vậy $∆ A B C$ đều chỉ cần AB = BC

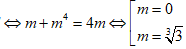
Kết hợp điều kiện ta có $m = \sqrt[3]{3}$ (thỏa mãn)

Lưu ý: có thể sử dụng công thức $\frac{b^{3}}{8 a} + 3 = 0$

$\frac{{(- 2 m)}^{3}}{8} + 3 = 0 \Leftrightarrow m^{3} = 3 m \Leftrightarrow m = \sqrt[3]{3}$

Câu 1:

Hàm số $y = x^{3} - 3 x + 1$ đạt cực đại tại $x$ bằng

Câu 2:

Tìm giá trị cực đại $y_{C Đ}$ của hàm số $y = - x^{4} + 2 x^{2} - 5$

Câu 3:

Hàm số $y = \frac{1}{3} x^{3} - 2 x^{2} + 4 x - 1$ có bao nhiêu điểm cực trị?

Câu 4:

Cho hàm số $y = x^{3} - 3 x^{2} + 2$ . Khẳng định nào sau đây đúng

Câu 5:

Khoảng cách giữa 2 điểm cực trị của đồ thị hàm số $y = x^{3} - 3 x$ là

Câu 6:

Cho hàm số $y = \frac{1}{4} x^{4} - 2 x^{2} + 3$ có đồ thị là $(C)$ . Diện tích tam giác có các đỉnh là các điểm cực trị của đồ thị $(C)$ là:

Câu 7:

Tìm tất cả các giá trị của tham số m để hàm số $y = \frac{1}{3} x^{3} - m x^{2} + (2 m - 1) x - 3$ có cực trị.

Câu 8:

Tìm tất cả các giá trị thực của tham số m để hàm số $y = m x^{4} + (m^{2} - 9) x^{2} + 10$ có 3 điểm cực trị

1000 bài tập trắc nghiệm ôn tập môn Toán có đáp án