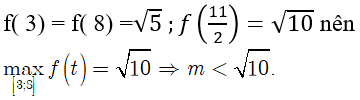Câu hỏi:
Tìm giá trị nguyên lớn nhất của m để: có nghiệm
A. 1
B. 2
C. 3
D. 4
Trả lời:
Điều kiện: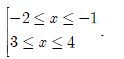 
Đặt t= x2- 2x; t’ = 2x- 2 và t’ =0 khi x= 1.
Bảng biến thiên
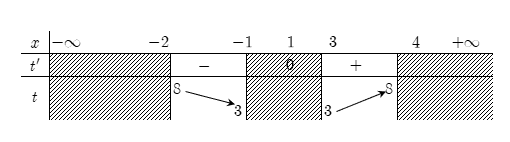
Dựa vào bảng biến thiên suy ra tập giá trị của t là [ 3; 8].
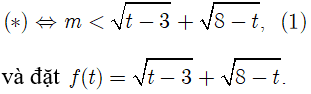
Để (* ) có nghiệm khi và chỉ khi ( 1) có nghiệm
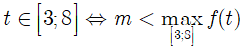
Xét hàm số
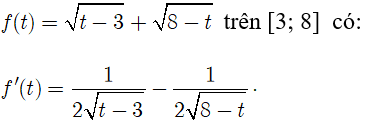
Cho f’ (t) =0 khi . Ta có:
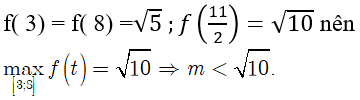
Vậy m ∈ (-∞; √10) sẽ thỏa mãn yêu cầu bài toán.
Chọn D.
Câu 1:
Cho hàm số y= x3-3x2-m-1 có đồ thị (C) . Giá trị của tham số m để đồ thị (C) cắt trục hoành tại ba điểm phân biệt lập thành cấp số cộng là
Câu 2:
Tìm tất cả các giá trị thực của tham số m sao cho hàm số đồng biến trên khoảng ?
Câu 4:
Cho hàm số có đồ thị (C) và đường thẳng d: y=x+m. Đường thẳng d cắt đồ thị (C) tại hai điểm A và B. Với C( -2; 5) , giá trị của tham số m để tam giác ABC đều là
Câu 5:
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x3-3( m+1) x2+ 12mx-3m+ 4 ( C) có hai điểm cực trị là A và B sao cho hai điểm này cùng với điểm C(-1; -9/2) lập thành tam giác nhận gốc tọa độ làm trọng tâm.
Câu 6:
Cho hàm số y= x4- 2( 1-m2) x2+ m+1. Tồn tại giác trị của m để hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số lập thành tam giác có diện tích lớn nhất . Khi đó khẳng định nào đúng?
