Tìm hai số tự nhiên a và b biết BCNN(a, b) – ƯCLN(a, b) = 35. A. (a; b) ∈ {(1; 36); (36; 1); (4; 9); (9; 4); (5; 40); (40; 5); (7; 42); (42; 7); (35; 70); (70; 35)}. B. (a; b) ∈ {(1; 36); (3
Câu hỏi:
Tìm hai số tự nhiên a và b biết BCNN(a, b) – ƯCLN(a, b) = 35.
A. (a; b) ∈ {(1; 36); (36; 1); (4; 9); (9; 4); (5; 40); (40; 5); (7; 42); (42; 7); (35; 70); (70; 35)}.
B. (a; b) ∈ {(1; 36); (36; 1); (4; 9); (9; 4); (5; 40); (40; 5); (7; 42); (42; 7); (14; 21); (21; 14)}.
C. (a; b) ∈ {(1; 36); (36; 1); (5; 40); (40; 5); (7; 42); (42; 7); (14; 21); (21; 14); (35; 70); (70; 35)}.
D. (a; b) ∈ {(1; 36); (36; 1); (4; 9); (9; 4); (5; 40); (40; 5); (7; 42); (42; 7); (14; 21); (21; 14); (35; 70); (70; 35)}.
Trả lời:
Đáp án đúng là D
Gọi ƯCLN(a, b) = d. Suy ra
ƯCLN(m, n) = 1 và m, n ∈ N*
Ta có BCNN(a, b) . ƯCLN(a, b) = ab
Suy ra
Mà BCNN(a, b) – UCLN(a, b) = 35
Do đó mnd – d = 35
Hay d(mn – 1) = 35
Suy ra mn – 1 ∈ Ư(35) = {1; 5; 7; 35}
Hay mn ∈ {2; 6; 8; 36}
+) Với d = 1 thì mn – 1 = 35 hay mn = 36
+) Với d = 5 thì mn – 1 = 7 hay mn = 8
+) Với d = 7 thì mn – 1 = 5 hay mn = 6
+) Với d = 35 thì mn – 1 = 1 hay mn = 2
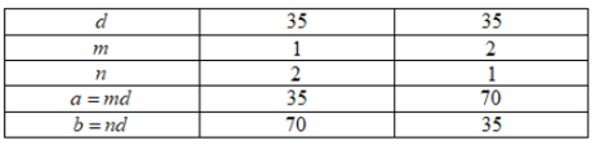
Khi đó ta có các cặp số thỏa mãn là (a; b) ∈ {(1; 36); (36; 1); (4; 9); (9; 4); (5; 40); (40; 5); (7; 42); (42; 7); (14; 21); (21; 14); (35; 70); (70; 35)}
Vậy ta chọn đáp án D.
