Tìm n ∈ ℕ* sao cho n2 – 14n – 256 là số chính phương.
Câu hỏi:
Tìm n ∈ ℕ* sao cho n2 – 14n – 256 là số chính phương.
Trả lời:
Giả sử n2 – 14n – 256 là số chính phương
Suy ra: n2 – 14n – 256 = a2 (a ∈ ℕ*).
⇔ n2 – 7n – 7n + 49 – 305 = a2
⇔ (n – 7)2 – a2 – 305 = 0
⇔ (n – 7 + a)(n – 7 – a) = 305
Vì a, n đều là số tự nhiên nên n – 7 – a < n – 7 + a
Mà 305 = 1.305 = 5.61
+ Nếu n – 7 + a = 305 và n – 7 – a = 1
⇒ n – a = 8; n + a = 312
⇒ n = 160
+ Nếu n – 7 + a = 61 và n – 7 – a = 5
⇒ n – a = 12; n + a = 68
⇒ n = 40.
Vậy n = 40 hoặc n = 160.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 2:
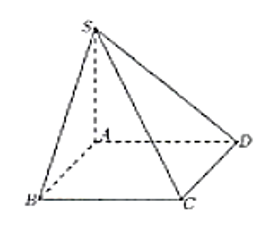
Cho hình chóp S.ABCD có đáy là hình vuông cạnh , SA vuông góc mặt phẳng đáy và SA = (minh họa hình bên). Góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng?
Xem lời giải »
Câu 3:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc mặt phẳng đáy và SB = . Tính thể tích khối chóp S.ABCD?
Xem lời giải »
Câu 4:
Cho tam giác ABC vuông tại A, biết AC = 5 cm, AB = 6 cm và = 45°. Tính các góc , và cạnh BC (sử dụng định lí côsin)?
Xem lời giải »
Câu 5:
Để viết các số tự nhiên liên tiếp từ 2 đến 125 thì cần dùng bao nhiêu chữ số?
Xem lời giải »
Câu 6:
Đồng hồ kim chỉ 1 giờ 15 phút tạo góc bao nhiêu độ?
Xem lời giải »
Câu 8:
Chứng tỏ rằng hai số 20142013 – 1 và 20142013 + 1 không thể đồng thời là hai số nguyên tố.
Xem lời giải »